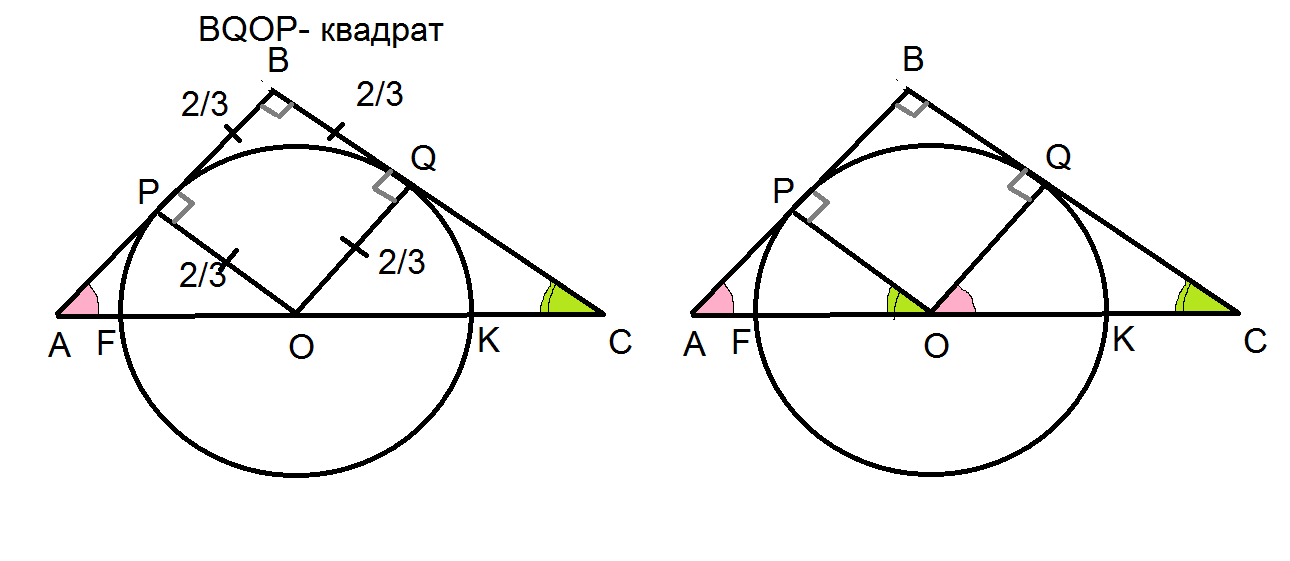
Задача 45621 Полуокружность радиуса 2/3, центр O...

slava191

2020-03-30 12:58:39

Полуокружность радиуса 2/3, центр O которой лежит на гипотенузе AC прямоугольного треугольника АВС, касается его катетов АВ и ВС в точках Р и Q соответственно.

а) Докажите, что треугольники АРО и OQC подобны.

б) Найдите площадь треугольника ABC, если OA = sqrt(5)/3. [16п3]

sova

2020-03-31 00:02:07

★

В прямоугольном треугольнике АВС
∠ ВАС= α
∠ ВСА= β
α + β =90 ° - cумма острых углов прямоугольного треугольника 90 °

Касательная перпендикулярна радиусу, проведенному в точку касания:
OP ⊥ AB
OQ ⊥ AC

В прямоугольном треугольнике РАО
∠ РАО= α , значит ∠ POA= β

В прямоугольном треугольнике CQО
∠ QCО= β , значит ∠ COQ= α

Δ APO ~ ΔCQO по двум углам.


AO=√5/3; AK=AO+OK=(√5/3)+(2/3)=(√5+2)/3
AF=AO-OF=(√5/3)-(2/3)=(√5-2)/3

По свойству касательной и cекущей, проведенных из точки А:
AP^2=AF*AK

AP^2=(√5-2)/3 * (√5+2)/3 = 1/9

AP=1/3

[b]AB[/b]=AP+PB=(1/3)+(2/3)=[b]1[/b]
Δ APO ~ ΔCQO
OP:QC=AP:OQ

QC=4/3
[b]BC[/b]=BQ+QC=(2/3)+(4/3)=[b]2[/b]

S_( ΔABC)=(1/2)AB*BC=(1/2)*1*2=1

О т в е т. S_( ΔABC)=1