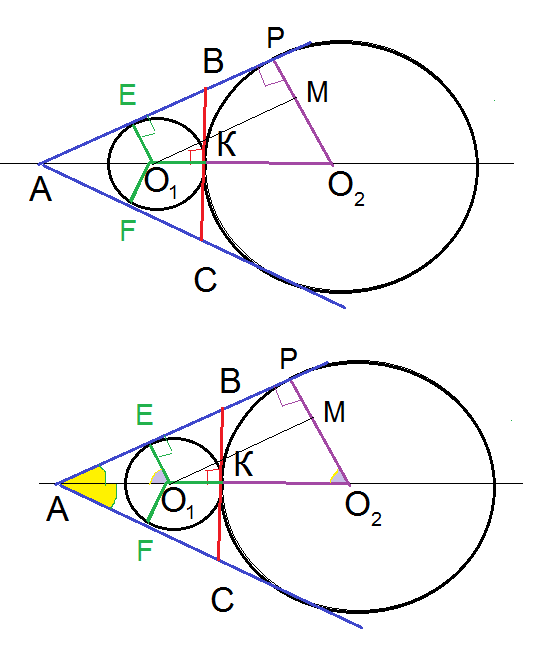
Задача 45619 Две касающиеся внешним образом в точке К...

slava191

2020-03-30 12:54:37

Две касающиеся внешним образом в точке К окружности, радиус одной из которых вдвое больше радиуса другой, вписаны в угол с вершиной А. Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.

а) Докажите, что АВ = АС.
б) Найдите радиус окружности, описанной около треугольника АВС, если АВ = sqrt(3). [16п2]

sova

2020-03-30 18:00:34

Две окружности вписаны в угол с вершиной А.
Радиусы O_(1)E и O_(1)F, проведенные в точки касания , [i]перпендикулярны [/i]сторонам угла.


По [i]свойству касательных[/i] к окружности, проведенных из одной точки, отрезки касательных равны:
[red]АE[/red]=[red]АF[/red]
и образуют [i]равные углы [/i]с прямой, проходящей через вершину А и центры окружностей.
Значит
центры O_(1) и O_(2) лежат на [i]биссектрисе[/i] угла А

BC - касательная к этим окружностям, проходящая через точку К,
значит О_(1)K ⊥ BC

AK - биссектриса и высота треугольника АВС, значит Δ АВС - равнобедренный и [b]АВ=АС[/b].

и AK - медиана Δ АВС ⇒ BK=CK

Прямоугольные треугольники
Δ AEO_(1)~ Δ APO_(2) по двум углам
( ∠ EAO_(2)- общий)
⇒ [b]∠ АО_(1)E= ∠ AO_(2)P [/b]

O_(1)EPO_(2) - прямоугольная трапеция.
O_(1)E=r
O_(2)E=2r

O_(1)O_(2)=3r

⇒ O_(1)M=r


Δ AEO_(1)= Δ O_(1)MO_(2) ⇒ [b] AO_(1)[/b]=O_(1)O_(2)=[b]3r[/b]

AE^2=AO^2_(1)-O_(1)E^2=(3r)^2-r^2=8r^2

[blue]AE=2√2*r[/blue]

AK=[b]AO_(1)[/b]+O_(1)K=[b]3r[/b]+r=4r

Δ AEO_(1)~ Δ ABC

[blue]AE:[/blue] AB=EO_(1):ВК

[blue]2√2*r[/blue]:√3=r:BK ⇒ BK=√3/(2√2)

BC=√(3/2)


По теореме Пифагора из треугольника АВК

AK^2=AB^2-BK^2=(√3)^2-(√3/(2√2))^2=3-(3/8)=21/8

AK=[m]\sqrt\frac{21}{8}[/m]

S_( Δ ABC)=(1/2)BC*AK

R=AB*BC*AC/4S_( Δ ABC)= AB^2/2AK=3/2sqrt(21/8)=sqrt(6/7)

О т в е т. [m]\sqrt\frac{6}{7}[/m]