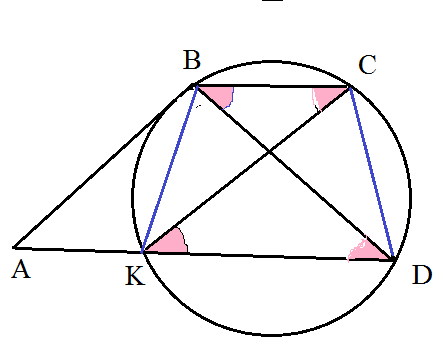
Задача 45509 Окружность проходит через вершины C ...

slava191

2020-03-28 16:00:21

Окружность проходит через вершины C и D трапеции ABCD, касается боковой стороны AB в точке B и пересекает большее основание AD в точке K. Известно, что AB = 5sqrt(3), BC = 5, KD = 10.

а) Докажите, что BD = sqrt(AD*BC)

б) Найти радиус окружности.

sova

2020-03-29 00:27:32

★

По свойству касательной и секущей, проведенных из точки А:
АК*KD=AB^2

Пусть АК=х, тогда AD=x+10

x*(x+10)=(5sqrt(3))^2
x^2+10x-75=0
D=100+4*75=400
x=5; x_(2) <0

AD=15

ABCK - параллелограмм, противоположные стороны BC и АК параллельны и равны ⇒ АВ=СK=5sqrt(3)

Трапеция KBCD вписана в окружность, значит BK=CD
и СК=BD=5sqrt(3)

BD^2=AD*BC - верно, так как [b](5sqrt(3))^2=15*5[/b]

Радиус окружности описанной около равнобедренной трапеции KBCD

Проводим высоту СM
MD=(KD-BC)/2=2,5
KM=KD-MD=7,5

СM^2=KC^2-KM^2=(5sqrt(3))^2-(7,5)^2=75/4

CD^2=CM^2+MD^2=(75/4)+(5/2)^2=25
CD=5

Находим радиус окружности, описанной около Δ КСD по формуле:

R=abc/4S

S_( ΔKCD)=(1/2)KD*CM=25sqrt(3)/2

[b]R=5[/b]

О т в е т.[b] 5[/b]