Задача 45423 Найти высоту, опущенную из вершины...

vk579418555

2020-03-27 12:47:20

Найти высоту, опущенную из вершины прямого угла треугольника, если известно, что его острый угол равен a и сумма катетов равна n.

sova

2020-03-27 12:53:16

★

( см. рис.)
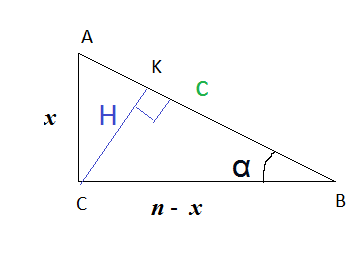
Пусть один катет х, второй (n-x)
sin α =[m]\frac{x}{c}[/m] ⇒ c=[m]\frac{x}{sin\alpha}[/m]

Теорема Пифагора
x^2+(n-x)^2=[m](\frac{x}{sin\alpha})^2[/m] ⇒

x^2+n^2-2nx+x^2- [m]\frac{x^2}{sin^2\alpha}=0[/m]

(2-[m]\frac{1}{sin^2\alpha}[/m])x^2-2nx+n^2=0

Квадратное уравнение.

[m]D=(-2n)^2-4\cdot(2-\frac{1}{sin^2\alpha })\cdot n^2=4n^2(\frac{2}{sin^2\alpha }-1)=[/m]
[m]=(\frac{2n}{sin\alpha }\cdot \sqrt{2-sin^2\alpha })^2[/m]

[m]x_{1}=\frac{n+n\sqrt{\frac{2}{sin^2\alpha} }-1}{2-\frac{1}{sin^2\alpha }};[/m]

[m]x_{2}=\frac{n-n\sqrt{\frac{2}{sin^2\alpha} }-1}{2-\frac{1}{sin^2\alpha }}.[/m]

[m]x_{1}=\frac{n\cdot sin\alpha(sin\alpha+\sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 };[/m]

[m]x_{2}=\frac{n\cdot sin\alpha(sin\alpha-\sqrt{2-sin^2\alpha}) }{2sin^2\alpha -1};[/m]


Из подобия прямоугольных треугольников СКВ и АСВ получаем пропорцию
H:x=(n-x):[m]\frac{x}{sin\alpha}[/m] ⇒ H=(n-x)*sin α

подставляем х и находим Н

[m]H=(n-\frac{n\cdot sin\alpha(sin\alpha+\sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]

или

[m]H=(n-\frac{n\cdot sin\alpha(sin\alpha-\sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]


[m]H=n\cdot (1-\frac{ sin\alpha(sin\alpha+\sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]

или

[m]H=n\cdot (1-\frac{sin\alpha(sin\alpha-\sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]


[m]H=n\cdot (\frac{2sin^2\alpha-1 - sin^2\alpha+sin\alpha \sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]

или

[m]H=n\cdot (\frac{2sin^2\alpha-1- sin^2\alpha-sin\alpha \sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]

[m]H=n\cdot (\frac{sin^2\alpha-1 +sin\alpha \sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]

или

[m]H=n\cdot (\frac{sin^2\alpha-1-sin\alpha \sqrt{2-sin^2\alpha}) }{2sin^2\alpha-1 })sin\alpha[/m]