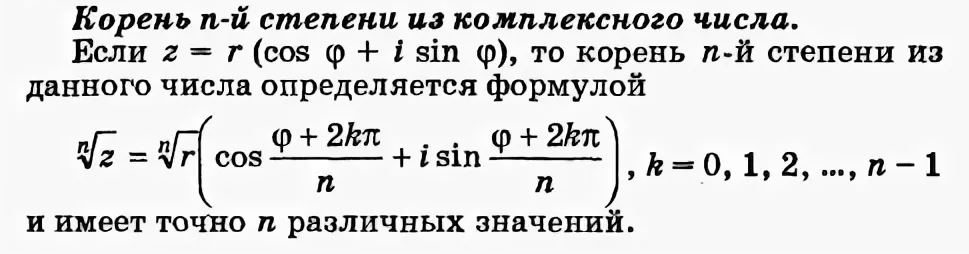Задача 45299 решить уравнение и изобразить все...

vk564985849

2020-03-24 14:39:45

решить уравнение и изобразить все решения на комплексной плоскости
z^3=1

sova

2020-03-24 14:47:26

★

1=cos0+isin0 - тригонометрическая форма комплексного числа z=1

Применяем формулу Муавра:

∛1=∛1*[m](cos\frac{0+2 \pi k}{3}+isin\frac{\frac{0+2\pi k}{3})[/m], k ∈ Z

при k=0
первый корень
z_(o)=1*[m](cos\frac{0}{3}+isin\frac{0}{3})=cos0+isin0=1[/m]

при k=1
второй корень
z_(1)=1*[m](cos \frac{0+2\pi}{3}+isin \frac{0+2\pi}{3})=1\cdot (cos\frac{2\pi}{3}+isin\frac{2\pi}{3})=-\frac{1}{2}+i\cdot (\frac{-\sqrt{3}}{2})[/m]

при k=2
третий корень
z_(2)=1*[m](cos\frac{0+4\pi}{3}+isin\frac{0+4\pi}{3})=1\cdot (cos\frac{4\pi}{3}+isin\frac{4\pi}{3})=\frac{1}{2}+i\cdot (\frac{-\sqrt{3}{2}})[/m]

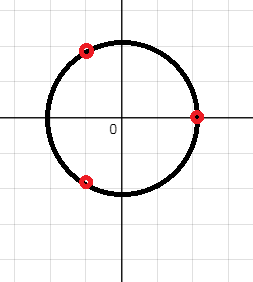
Корни расположены на окружности радиуса 1, делят окружность на три равные части, между точками углы в 120 градусов

первый корень z_(o) - точка с координатами (1;0)

второй корень z_(1) -точка во второй четверти, с координатами

[m](-\frac{1}{2};-\frac{\sqrt{3}}{2})[/m]

между ними угол в 120 градусов.

третий корень z_(2) -точка в третьей четверти, с координатами
[m](-\frac{1}{2};-\frac{\sqrt{3}}{2})[/m]

между ними угол в 120 градусов.