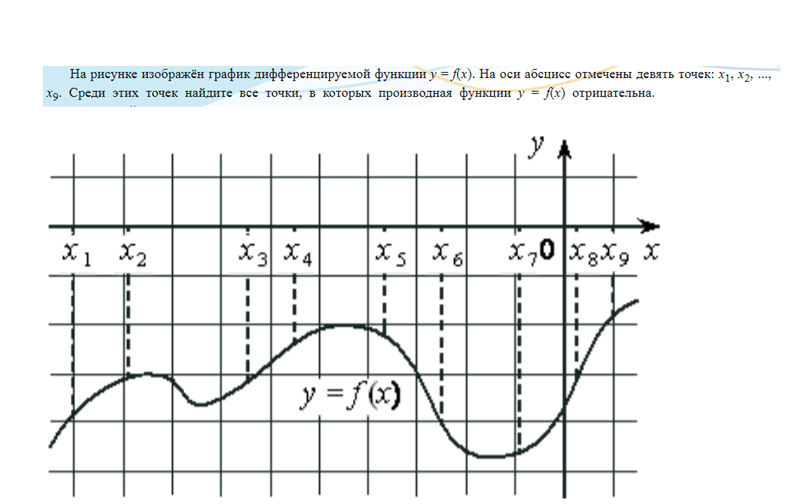
Задача 45235 Решите пожалуйста задание....

vk288952222

2020-03-23 10:38:46

Решите пожалуйста задание.

sova

2020-03-23 10:43:30

★

Геометрический смысл производной в точке:

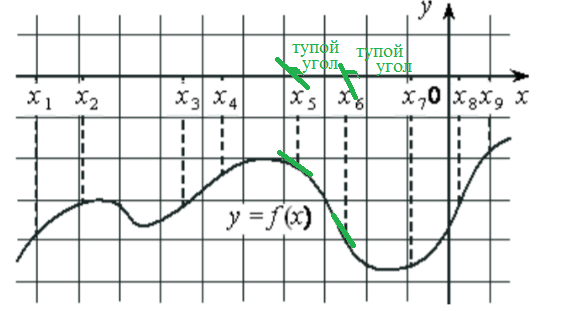
f`(x_(o))=k(касательный)=tg α

α угол α , который образует касательная(к графику функции в этой точке ) с положительным направлением оси Ох


f`(x_(o)) < 0 ⇔ tg α < 0 значит угол α , который образует касательная - [i]тупой.[/i]

Таких точек - две


О т в е т. x_(5) и x_(6)