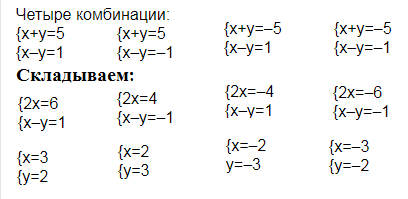Задача 44974 Решите систему...
Условие
(х)^2+ху+(у)^2=19
(х)^4+(х)^2(у)^2+(у)^4=133
Решение
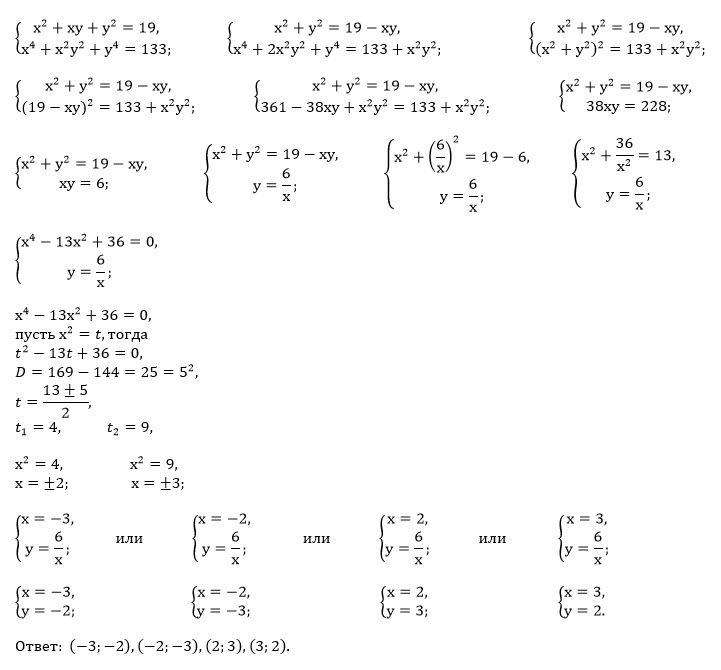
Все решения
[m]x^2+y^2=u[/m]
[m]x\cdot y=v[/m]
тогда
[m]x^4+y^4=(x^2+y^2)^2-2x^2y^2=u^2-2v^2[/m]
[m]x^4+x^2y^2+y^4==u^2-2v^2+v^2=u^2-v^2[/m]
Система принимает вид:
{[m]u+v=19[/m]
{[m]u^2-v^2=133[/m]
{[m]u+v=19[/m]
{[m](u-v)\cdot (u+v)=133[/m]
{[m]u+v=19[/m]
{[m](u-v)\cdot 19=133[/m]
{[m]u+v=19[/m]
{[m]u-v=7[/m]
Складываем:
{[m]2u=26[/m]
{[m]u-v=7[/m]
{[m]u=13[/m]
{[m]v=u-7=6[/m]
Обратный переход:
{[m]x^2+y^2=13[/m]
{[m]x\cdot y=6[/m]
Второе умножаем на 2:
{[m]x^2+y^2=13[/m]
{[m]2\cdot x\cdot y=12[/m]
Складываем:
[m](x+y)^2=25[/m] ⇒ [m] x+y=5 [/m] или [m]х+у=-5[/m]
Вычитаем
[m](x-y)^2=1[/m] ⇒ [/m] x-y=1[m] или [/m]x-y= -1[m]