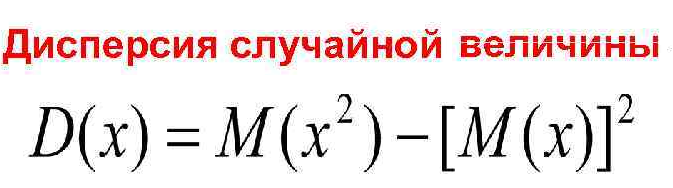Задача 44939 ...

vk515828602

2020-03-11 14:35:39

Вопрос №7.

Дана функция распределения вероятностей неперерывной случайной величины ξ:

[m]
F_ξ(x) =
\begin{cases}
0, & x \leq 0, \\
4x^2, & 0 < x \leq \frac{1}{2}, \\
1, & x > \frac{1}{2}.
\end{cases}
[/m]

Для случайной величины ξ найдите значение выражения 9D(ξ), где D(ξ) — это дисперсия этой случайной величины.

sova

2020-03-11 14:49:49

★

M( ξ )= ∫ ^(+ ∞ )_(- ∞ )xf_( ξ )(x)dx

f_( ξ )(x)=F`_( ξ )(x)

[m]\left\{\begin{matrix} 0,& x\leq 0\\ 8x, &0 < x \leq \frac{1}{2} \\ 0, & x>\frac{1}{3} \end{matrix}\right.[/m]

Так как функция задана на трех интервалах, то считаем интеграл как сумму интегралов на каждом интервале:

M( ξ )= ∫ ^(0)_(- ∞ )x[b]0[/b]dx+ ∫ ^([m]\frac{1}{2}[/m] )_(0 )x*(8x)dx+ ∫^(+ ∞ ) _([m]\frac{1}{2}[/m] )x*[b]0[/b]dx=

= ∫ ^([m]\frac{1}{2}[/m] )_(0 )x*(8x)dx=

=(8[m]\frac{x^3}{3}[/m])| ^([m]\frac{1}{2}[/m] )_(0 )=8*([m]\frac{1}{2}[/m])^3=[m]\frac{1}{3}[/m]

M( ξ^2 )= ∫ ^(0)_(- ∞ )x^2[b]0[/b]dx+ ∫ ^([m]\frac{1}{2}[/m] )_(0 )x^2*(8x)dx+ ∫^(+ ∞ ) _([m]\frac{1}{2}[/m] )x^2*[b]0[/b]dx=

= ∫ ^([m]\frac{1}{2}[/m] )_(0 )x^2*(8x)dx=

=(8[m]\frac{x^4}{4}[/m])| ^([m]\frac{1}{2}[/m] )_(0 )=2*([m]\frac{1}{2}[/m])^4=[m]\frac{1}{8}[/m]

D( ξ )=(M( ξ^2 )-(M( ξ))^2 =[m]\frac{1}{8}[/m]-([m]\frac{1}{3}[/m])^2=[m]\frac{1}{72}[/m]

9*D( ξ )=[m]\frac{1}{8}[/m]