Задача 44898 Ребро куба ABCDA B C D 1 1 1 1 равно 2...

vk396216921

2020-03-10 12:05:26

Ребро куба
ABCDA B C D 1 1 1 1
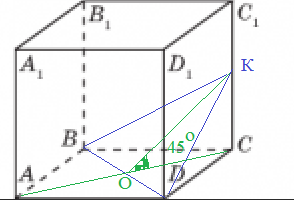
равно 2 см. Через диагональ основания BD под углом 45° к
плоскости основания проведена плоскость BDK, пересекающая боковое ребро в точке K.
Найдите площадь треугольника BDK.

sova

2020-03-10 16:09:18

★

S_( Δ BDK)=BD*KO/2

BD=AC=2sqrt(2) - диагонали квадрата АВСD со стороной 2
ОС=СК=АС/2=sqrt(2)
По теореме Пифагора из ΔОСК
KO^2=(sqrt(2))^2+sqrt(2)^2=4
KO=2

S_( Δ BDK)=[b]2sqrt(2)[/b]