Задача 44873 Через точку окружности основания...

slava191

2020-03-08 22:04:25

Через точку окружности основания цилиндра проведены два сечения: одно через ось цилиндра, а второе параллельно ей. Угол между плоскостями сечений равен 45°. Площадь боковой поверхности цилиндра равна 18Pisqrt(2). Найдите меньшую из площадей данных сечений. [Ларин 8]

sova

2020-03-09 00:09:57

★

Сечение через ось цилиндра - это осевое сечение, проведенное через диаметр АВ=2R

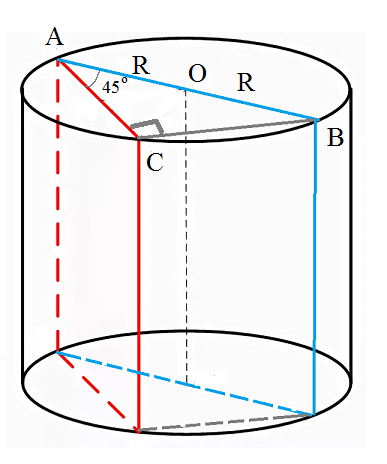
Второе сечение проходит через хорду AC, образующую с диаметром AB угол 45 °

Угол опирающийся на диаметр ∠ АСВ=90 °

Из прямоугольного треугольника АВС:

AC=AB*cos45 °=[b]R*sqrt(2)[/b]


S_(бок. пов цилиндра)=2π*R*H

По условию: S_(бок. пов цилиндра)=18π*sqrt(2)

2π*R*H=18π*sqrt(2)

[b]R*H[/b]=9*sqrt(2)

S_(cечения)=АС*H=R*sqrt(2)*H=[b]R*H[/b]*sqrt(2)=9sqrt(2)*sqrt(2)=

=[b]18[/b]

О т в е т.[b]18[/b]