Задача 44791 ...
Условие
[red][r][b]Проверьте пожалуйста мои ответы: [/red]
А2) √61
А3) 36√7
[green]И решите А4 [/b][/r][/green]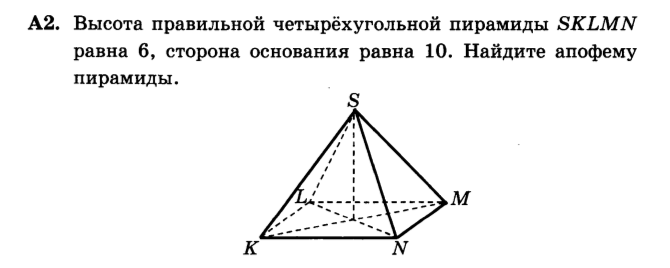
математика 10-11 класс
999
Решение
★
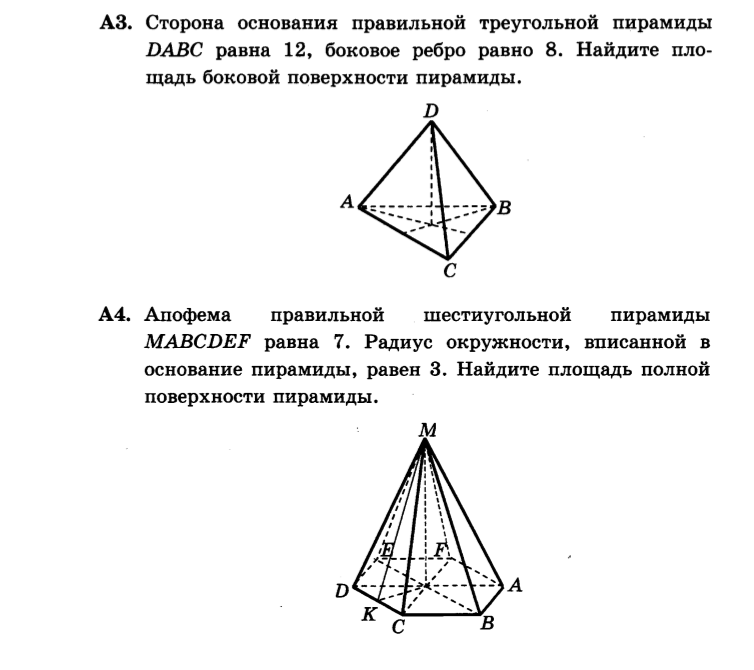
радиус окружности, вписанной в правильный шестиугольник со стороной а, это высота одного из шести правильных треугольников со стороной а:
r=asqrt(3)/2
a=2r/sqrt(3)=2*3/sqrt(3)=2sqrt(3)
S_(полн)=S_(осн)+S_(бок)=
=6*S_( Δ)+6*(a*h/2)=[b] [h--апофема, h=7][/b]
=6*(1/2)*a^2sin60^(o)+(6*2sqrt(3)*7/2)
=3*(2sqrt(3))^2*(sqrt(3)/2)+42sqrt(3)=(18+42)sqrt(3)=[b]50sqrt(3)[/b]
A2 - верно
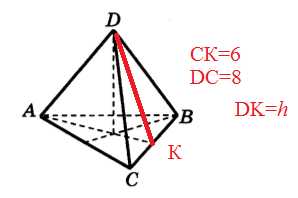
А3
Апофема h^2=DC^2+CK^2=8^2+6^2=64+36=100
S_(бок)=3*S_( Δ)=3*(12*10)/2=180