Задача 44782 Система уравнений. оформите формулами,...
Условие
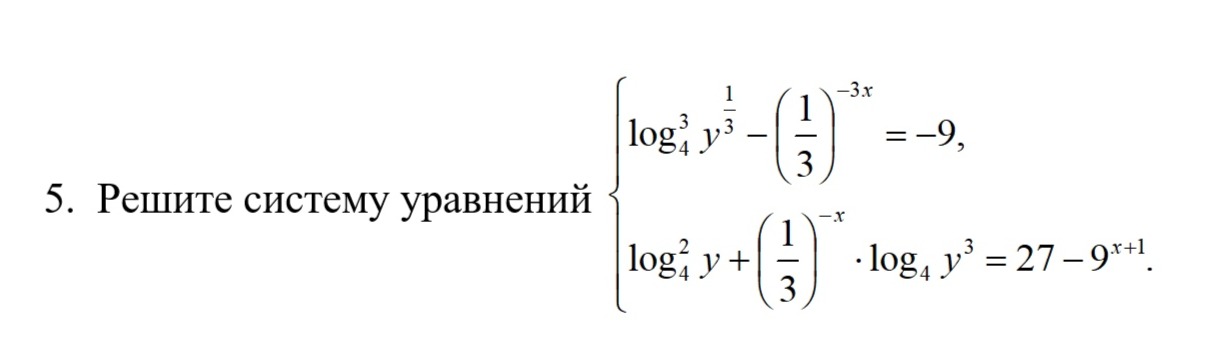
Решение
[m]log^{3}_{4}y^{\frac{1}{3}}=(log_{4}y^{\frac{1}{3}})^{3}=(\frac{1}{3}log_{4}y)^3=\frac{1}{27}log^3_{4}y[/m]
[i]Замена переменной:[/i]
[m]log_{4}y=u[/m]
[m](\frac{1}{3})^{-x}=v[/m]
v>0
[m](\frac{1}{3})^{-x}=3^{x}[/m]
[m]9^{x}=v^2[/m]
[m]\left\{\begin{matrix} \frac{1}{27}u^{3}-v^{3}=-9 & \\ u^2+v\cdot 3u =27-9v^{2}& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} (\frac{1}{3}u)^{3}-v^{3}=-9 & \\ u^2+v\cdot 3u +9v^{2}=27& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} (\frac{1}{3}u-v)\cdot (\frac{1}{9} u^2+v\cdot\frac{1}{3}u +v^{2})=-9 & \\ \frac{1}{9}u^2+\frac{1}{3}u\cdot v +v^{2}=3& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} (\frac{1}{3}u-v)\cdot ( 3)=-9 & \\ u^2+v\cdot 3u +9v^{2}=27& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}\frac{1}{3}u-v=-3 & \\ u^2+v\cdot 3u +9v^{2}=27& \end{matrix}\right.[/m]
Применяем [i]способ подстановки[/i]:
[m]\left\{\begin{matrix} v=\frac{1}{3}u+3 & \\ u^{2}+(\frac{1}{3}u+3)\cdot 3\cdot u +9(\frac{1}{3}u+3)^{2}=27& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} v=\frac{1}{3}u+3 & \\ 3u^{2}+27u+54=0& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} v=\frac{1}{3}u+3 & \\ 3\cdot (u^2+9u+18)=0&
\end{matrix}\right.[/m]
[m]\left\{\begin{matrix} v=\frac{1}{3}(-3)+3 & \\ u=-3; u=-6&
\end{matrix}\right.[/m]
[m]\left\{\begin{matrix} v=2 & \\ u=-3&
\end{matrix}\right.[/m]
[m]\left\{\begin{matrix} v=1 & \\ u=-6&
\end{matrix}\right.[/m]
Обратный переход
[m]\left\{\begin{matrix} 3^{x}=2 & \\ log_{4}y=-3&
\end{matrix}\right.[/m]
[m]\left\{\begin{matrix} 3^{x}=1 & \\ log_{4}y=-6&
\end{matrix}\right.[/m]
[m]\left\{\begin{matrix} x=log_{3}2 & \\ y=4^{-3}&
\end{matrix}\right.[/m]
[m]\left\{\begin{matrix} x=0 & \\ y=4^{-6}&
\end{matrix}\right.[/m]
решения входят в ОДЗ
О т в е т. ([m]0;\frac{1}{4096})[/m]; ([m]log_{3}2;\frac{1}{64})[/m]