Задача 44781 Уравнение и неравенства 2. оформите...
Условие
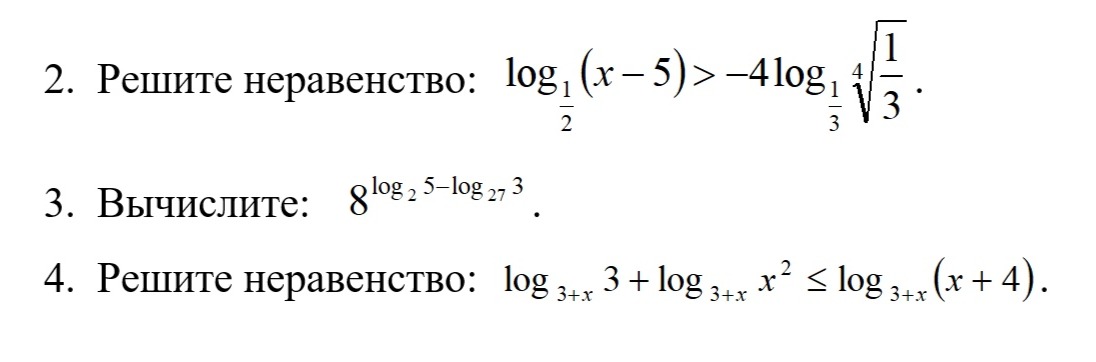
Решение
[m]log_{\frac{1}{3}}\sqrt[4]{\frac{1}{3}}=log_{\frac{1}{3}}(\frac{1}{3})^{\frac{1}{4}}=\frac{1}{4}log_{\frac{1}{3}}(\frac{1}{3})=\frac{1}{4}[/m]
Неравенство принимает вид:
[m]log_{\frac{1}{2}}(x-5)> -4\cdot \frac{1}{4}[/m]
так как
[m]-1=log_{\frac{1}{2}}2[/m]
[m]log_{\frac{1}{2}}(x-5)> log_{\frac{1}{2}}2[/m]
Логарифмическая функция с основанием [m]0 <
\frac{1}{2} < 1[/m] убывающая
[m]\left\{\begin{matrix} x-5>0& \\ x-5<2& \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} x>5& \\ x<7& \end{matrix}\right.[/m]
О т в е т. [b](5;7)[/b]
3.
[m]log_{27}3=log_{3^{3}}3=\frac{1}{3}log_{3}3=\frac{1}{3}[/m]
[m]8^{log_{2}5-log_{27}3}=(2^{3})^{log_{2}5-\frac{1}{3}}=2^{3log_{2}5-1}=2^{log_{2}5^3}\cdot2^{-1}=\frac{125}{2}=62,5[/m]
4.
[red]ОДЗ:[/red]
{x^2>0 ⇒ x ≠ 0
{3+x>0 ⇒ x>-3
{3+x ≠ 1 ⇒ x ≠ -2
{x+4>0 ⇒ x>-4
[red]x ∈ (-3;-2)U(-2;0)U(0;+ ∞ )[/red]
Заменим[i] сумму [/i]логарифмов логарифмом [i]произведения
[/i]
log_(3+x)(3x^2) ≤ log_(3+x)(x+4)
Рассматриваем[i] два случая[/i]:
1) [i]Основание логарифмической функции[/i]
0<3+x<1 ⇒[green] -3 < x < -2[/green]
логарифмическая функция [i]убывающая[/i]
3x^2 ≥ x+4
3x^2-x-4 ≥ 0
D=1-4*3*(-4)=49
x_(1)=(1-7)/6=-1; x_(2)=(1+7)/6=4/3
x ≤ -1 или х ≥ 4/3
Множества -3 < x < -2 и x ≤ -1 пересекаются
О т в е т первого случая с учетом ОДЗ
[b](-3;-2)[/b]
2)
[i]Основание логарифмической функции[/i]
3+x>1 ⇒ [green]x> -2[/green]
логарифмическая функция [i] возрастающая[/i]
3x^2 ≤ x+4
3x^2-x-4 ≤ 0
D=1-4*3*(-4)=49
x_(1)=(1-7)/6=-1; x_(2)=(1+7)/6=4/3
[b]-1 ≤ x ≤ 4/3[/b]
О т в е т второго случая с учетом ОДЗ
[b][-1;0)U(0;4/3][/b]
Объединяем ответы:
[b](-3;-2)U[-1;0)U(0;4/3][/b]