Задача 44780 Уравнения 1. оформите формулами,...
Условие
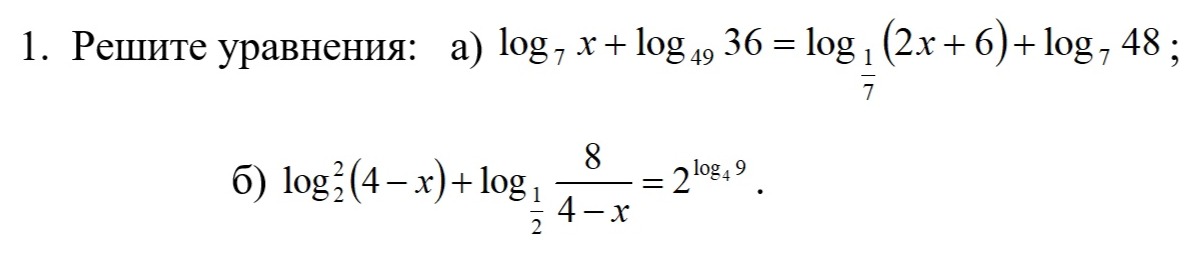
Решение
[red]ОДЗ:[/red]
{x>0
{2x+6>0 ⇒ x > -3
[red]x>0 [/red]
[m]log_{7}x+log_{7^{2}}6^{2}=log_{7^{-1}}(2x+6)+log_{7}48[/m]
По формуле:
[r][m]log_{a^{k}}b^{n}=\frac{n}{k}log_{a}b[/m], a >0; b>0; a ≠ 1[/r]
[m]log_{7}x+\frac{2}{2}log_{7}6=-log_{7}(2x+6)+log_{7}48[/m]
[m]log_{7}x+log_{7}6+log_{7}(2x+6)=log_{7}48[/m]
По формуле:
[r][m]log_{a}(bc)=log_{a}b+log_{a}c[/m], a >0; b>0; c>0 a ≠ 1[/r]
[m]log_{7}(x\cdot 6\cdot (2x+6))=log_{7}48[/m]
[m]x\cdot 6\cdot (2x+6)=48[/m]
[m]x\cdot (2x+6)=8[/m]
[m]2x^{2}+6x-8=0[/m]
[m]x^{2}+3x-4=0[/m]
[m]D=9+16=25[/m]
[m]x=\frac{3-5}{2}=-1[/m]; [m]x=\frac{3+5}{2}=4[/m]
x=-1 не входит в ОДЗ
О т в е т. [b]4[/b]
[b]б)[/b]
[red]ОДЗ[/red]: 4-x >0
[red]x <4[/red]
По формуле:
[r][m]log_{a^{k}}b^{n}=\frac{n}{k}log_{a}b[/m], a >0; b>0; a ≠ 1[/r]
[m]log_{4}9=log_{2^2}3^{2}=log_{2}3[/m]
По формуле:[m] a^{log_{a}b}=b[/m]a >0; b>0; a ≠ 1
[m]2^{log_{4}9}=2^{og_{2}3}=3[/m]
По формуле:
[r][m]log_{a}\frac{b}{c}=log_{a}b-log_{a}c[/m], a >0; b>0; c>0 a ≠ 1[/r]
[m]log^{2}_{2}(4-x)+log_{\frac{1}{2}}8-log_{\frac{1}{2}}(4-x)=3[/m]
[m]log^{2}_{2}(4-x)+log_{2^{-1}}8-log_{2^{-1}}(4-x)=3[/m]
По формуле:
[r][m]log_{a^{k}}b^{n}=\frac{n}{k}log_{a}b[/m], a >0; b>0; a ≠ 1[/r]
[m]log^2{2}(4-x)-log_{2}8+log_{2}(4-x)-3=0[/m]
[m]log_{2}8=3[/m]
[m]log^{2}_{2}(4-x)+log_{2}(4-x)-6=0[/m]
Квадратное уравнение относительно
[m]log_{2}(4-x)[/m]
Лучше ввести новую переменную
[m]log_{2}(4-x)=t[/m]
[m]t^{2}+t-6=0[/m]
[m]D=25[/m]
[m]t_{1}=-3[/m] или [m] t_{2}=2[/m]
Обратный переход
[m]log_{2}(4-x)=-3[/m] или [m] log_{2}(4-x)=2[/m]
[m]4-х=2^{-3}[/m] или [m] 4-x=2^{2}[/m]
[m]4-x=\frac{1}{8} [/m] или [m] x=0 [/m]
[m]x=4-\frac{1}{8}[/m]
[m]x=\frac{31}{8}[/m]
Оба корня удовлетворяют ОДЗ
О т в е т. [m]0; \frac{31}{8} [/m]