Задача 44702 Исследовать функцию, при помощи...

vk463769117

2 марта 2020 г. в 18:20

Исследовать функцию, при помощи производной простроить график.

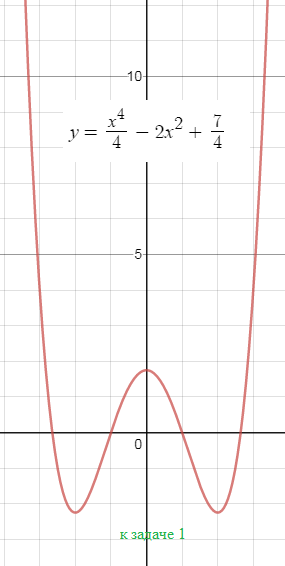
1) у=1\4х²–2x²+7\4
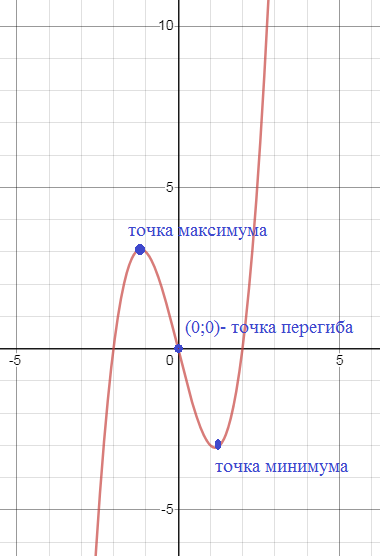
2) у=х³–4x

10–11 КЛАСС (КОЛЛЕДЖ)

sova

2 марта 2020 г. в 18:29

1.Область определения (– ∞;+ ∞)
Функция четная
y(–x)=(1/4)·(–x)⁴–2·(–x)²+(7/4)=(1/4)x⁴–2x²+(7/4)

y`=x³–4x

y`=0

x³–4x=0

x·(x²–4)=0

x=0; x= ± 2

__–__ (–2) _+___ (0) __–__ (2) __+_

y`< 0 на(– ∞; –2) и на (0;2)

значит функция убывает на(– ∞; –2) и на (0;2)


y`>0 на (– 2; 0) и на (2;+ ∞)

значит функция возрастает на
(– 2; 0) и на (2;+ ∞)

х=0 – точка максимума, производная меняет знак с + на –

x= ± 2 – точки минимума, производная меняет знак с – на +


y``=3x²–4

3x²–4=0
x²=4/3
x= ± 2√3/3

y``>0 на (– ∞; –2√3/3) и на (2√3/3;+ ∞)
функция выпукла вниз

y``< 0 на(–2√3/3;2√3/3)
функция выпукла вверх

2.
Область определения (– ∞;+ ∞)

f`(x)=3x2–4
f`(x)=0

3x2–4=0

х= ± 2√3/3

Знак производной
_+_ (–2√3/3) __–__ (2√3/3) __+__

y`< 0 на(–2√3/3;2√3/3)

значит функция убывает на(–2√3/3;2√3/3)


y`>0 на(– ∞; –2√3/3) и на (2√3/3;+ ∞)

значит функция возрастает на
(– ∞; –2√3/3) и на (2√3/3;+ ∞)

х=–2√3/3 – точка максимума, производная меняет знак с + на –

x=2√3/3 – точка минимума, производная меняет знак с – на +


y``=6x

y`` < 0 при х < 0

кривая выпукла вверх на (– ∞;0)

y``>0 при x > 0

кривая выпукла вниз на (0;+ ∞)

х=0 – точка перегиба
см. рис