Задача 44630 Обчисліть інтеграли, користуючись...
Условие
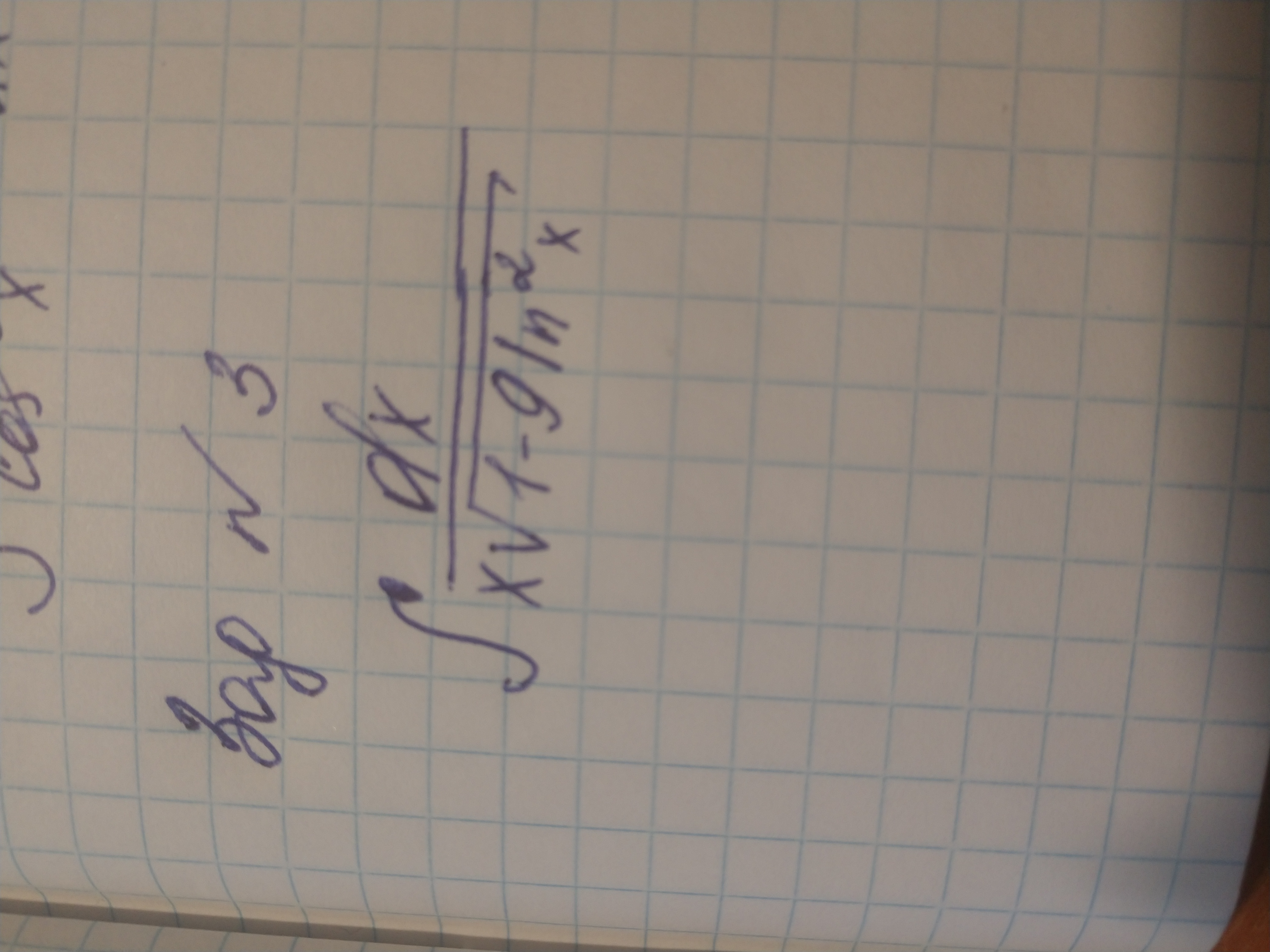
математика ВУЗ
589
Все решения
3lnx=u
d(3lnx)=(3lnx)`dx=3*(dx/x)
d(3lnx)=3dx/x
Умножаем dx на 3 и делим на (1/3), которую вынесем за знак интеграла.
[i]В квадратных скобках подсказка, какой табличный интеграл получим[/i] и ее можно не записывать
[m]\int \frac{dx}{x\sqrt{1-9ln^2x}}=\frac{1}{3}\int \frac{3dx}{x}\frac{1}{\sqrt{1-(3lnx)^2}}=[\int \frac{du}{\sqrt{1-u^2}}=]=\int \frac{d(3lnx)}{\sqrt{1-(3lnx)^2}}[/m]
=[b]arcsin(3lnx)+C[/b]