Задача 44616 Извините пожалуйста, что уже задавал...
Условие
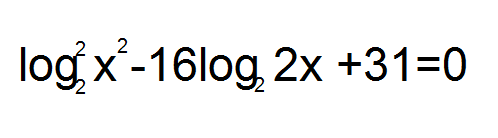
Решение
Формула логарифма степени:
log_(a)b^(n)=nlog_(a)b если a>0; b>0
Эта же формула для x неизвестного знака ( как + так -)
требует модуля:
log_(2)x^2=2log_(2)|x|
Но если вначале решения Вы указали ОДЗ уравнения:
{2x>0 ⇒ x>0
{x^2 >0 ⇒ x ≠ 0
то формула примет вид:
log_(2)x^2=2log_(2)|x|=2log_(2)x
Поэтому можно написать:
в условиях ОДЗ
log^2_(2)x^2=(2log_(2)|x|)^2=4log^2_(2)|x|=4log^2_(2)x
и
log_(2)2x=log_(2)2+log_(2)x=1+log_(2)x
Уравнение принимает вид:
4log^2_(2)x-16*(1+log_(2)x)+31=0
Далее кв. уравнение и корни