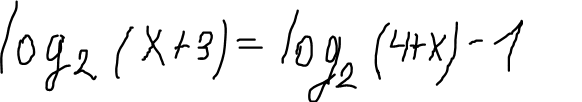Задача 44611 Решите уравнения пожалуйста.А во 2...
Условие
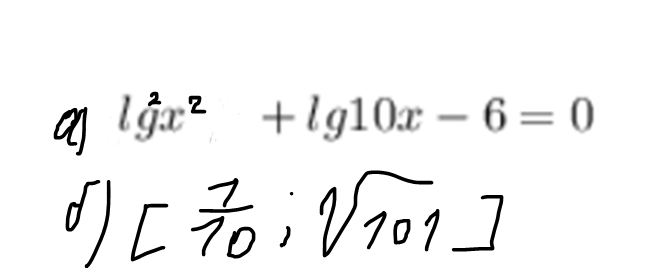
математика
603
Решение
★
lgx^2=2lgx
lg^2x^2=(2lgx)^2=4lg^2x
4lg^2x+1+lgx-6=0
4lg^2x+lgx-5=0
D=1-4*4*(-5)=81
lgx=-5/4; lgx=1
x=10^(-5/4) или x=10
10 ∈ [1/10;sqrt(101)]
10^(-5/4) < 10^(-1)=0,1
10^(-5/4) ∉ [1/10;sqrt(101)]
б)
log_(2)(x+3)+1=log_(2)(4+x)
1=log_(2)2
log_(2)(x+3)+log_(2)2=log_(2)(4+x)
log_(2)(x+3)*2=log_(2)(4+x)
(x+3)*2=4+x
2x+6=x+4
x=-2
Проверка:
log_(2)(-2+3)+1=log_(2)(4-2)
log_(2)1+1=log_(2)2
1=1 - верно
О т в е т. -2