Задача 44597 Две системы. (Еще) Распишите (кратко)...
Условие
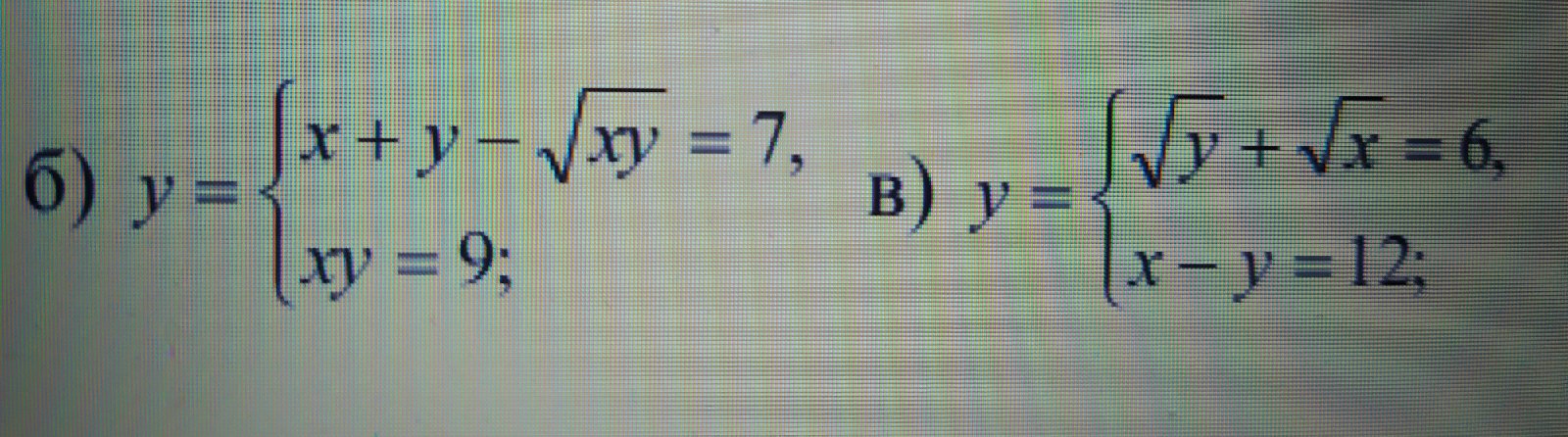
предмет не задан
588
Решение
★
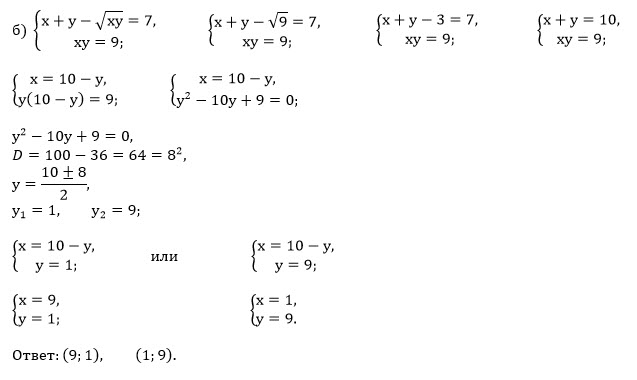
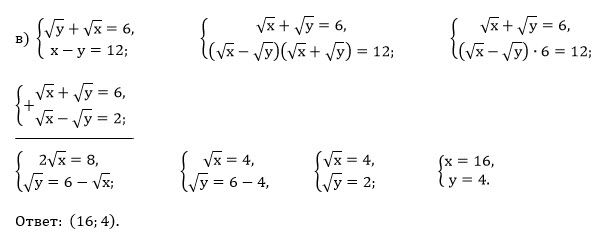
Все решения
Замена
x+y=u
sqrt(xy)=v;
xy ≥ 0 ⇒ (x;y) в первой или третьей четверти
v ≥ 0
{u-v=7
{v^2=9 ⇒ так как v ≥ 0, v=3
и подставляем в первое
u=10
{x+y=10
{xy=9
[b]x=1;y=9[/b]
или
[b]x=9;y=1[/b]
О т в е т.(1;9);(9;1)
2) x-y=(sqrt(x)-sqrt(y))*(sqrt(x)+sqrt(y))
x-y=6*(sqrt(x)-sqrt(y))
Cистема примет вид:
{sqrt(y)+sqrt(x)=6
{6*(sqrt(x)-sqrt(y))=12 Делим на 2
{sqrt(y)+sqrt(x)=6
{sqrt(x)-sqrt(y)=2
Складываем:
2sqrt(x)=8
sqrt(x)=4 ⇒[b] x=16[/b]
y=x-12=16-12=[b]4[/b]
О т в е т.(16;4)