Задача 44502 ...

sova

2020-02-24 13:07:09

★

x^2+(a-6)^2=|x+a-6|+|x-a+6|

a-6=b

x^2+b^2=|x+b|+|x-b|

[b](- ∞ ;-b)[/b]
x^2+b^2=-x-b-x+b ⇒ x^2+2x+b^2=0 D=4-4b^2

Это уравнение имеет один или два корня при D ≥ 0

Если получаем два корня, то один должен быть "лишним",
т. е не принадлежащим (- ∞ ;-b)


[b](-b;b)[/b]
x^2+b^2=x+b-x+b ⇒ x^2+b^2-2b=0

x= ± sqrt(2b-b^2)

2b-b^2 ≥ 0

те же указания

[b](b;+ ∞ )[/b]
x^2+b^2=x-b+x+b ⇒ x^2-2x+b^2=0 ⇒ D=4-4b^2

те же указания

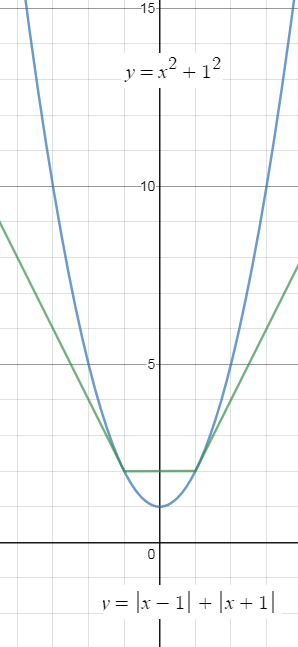
Можно графически:
x^2+b^2=|x+b|+|x-b|

y=x^2+b^2 - парабола, ветви вверх

y=|x+b|+|x-b| ломаная.

cм рис. для b=1

Из рис. видно, что один корень в том случае, когда прямая y=|x+b|+|x-b| касается параболы y=x^2+b^2 в вершине:

Вершина в точке (0;b^2)

Значит уравнение прямой y=b^2

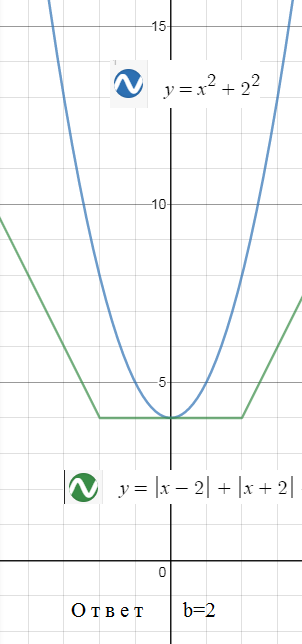
b^2=2b

b=0; [b]b=2[/b] ( см. рис. для b=2)

⇒
a-6=0; [b]a-6=2[/b]
a=6; a=8

О т в е т. 6;8