Задача 44459 (4cos^2x-1)sqrt(49Pi^2-x^2) = 0, [20;...
Условие
Решение
[red]Первый множитель равен 0:[/red]
{4cos^2x-1=0 ⇒ cos^2x=1/4 ⇒ cosx= ± (1/2)
{49π^2-x^2 ≥ 0 ⇒ (7π-x)*(7π+x) ≥ 0 ⇒ -7π ≤ x ≤ 7π
Так как уравнение
cosx= 1/2
имеет корни в первой и в четвертой четвертях:
x=(π/3)+2πn, n ∈ Z и х=- (π/3) +2πm, m ∈ Z
а уравнение
сosx=-1/2
имеет корни во второй и третьей четвертях:
x= (2π/3)+2πn, n ∈ Z и х= - (2π/3) +2πm, m ∈ Z
, то корни уравнения можно записать в виде:
x= (π/3)+πk, k ∈ Z или x= -(π/3)+πm, m ∈ Z
[i]Второму неравенству[/i] системы удовлетворяют корни:
при k=-7;-6; -5;-4;-3;-2;-1;0;1;2;3;4;5;6
и
при m=-6; -5;-4;-3;-2;-1;0;1;2;3;4;5;6;7
[red]о т в е т первого случая[/red]
x= (π/4)+πk, k ∈ Z
k=-7;-6; -5;-4;-3;-2;-1;0;1;2;3;4;5;6
x=- - (π/4)+πm, m ∈ Z
m=-6; -5;-4;-3;-2;-1;0;1;2;3;4;5;6;7
[red]Второй множитель равен 0[/red]
sqrt(49π^2-x^2)=0 ⇒ 49π^2-x^2=0 ⇒ x= ± 7π
[red]о т в е т второго случая[/red] x= ± 7π
б)
Так как -7π ≤ x ≤ 7π
и 7π<25
то выбираем корни, принадлежащие [20;7π]
(π/3)+6π< 20, так как 19*π< 60
и
6π<20<7π
Указанному промежутку [15;20] принадлежат корни:
[b]x_(1)[/b]=-(π/3)+7π=[b]20π/3[/b]
[b]x_(2)=7π[/b]
cм. рис.
О т в е т.
x= (π/3)+πk, k ∈ Z
k=-7;-6; -5;-4;-3;-2;-1;0;1;2;3;4;5;6
x=- (π/3)+πm, m ∈ Z
m=-6; -5;-4;-3;-2;-1;0;1;2;3;4;5;6;7
б)[b] 20π/3; 7π[/b]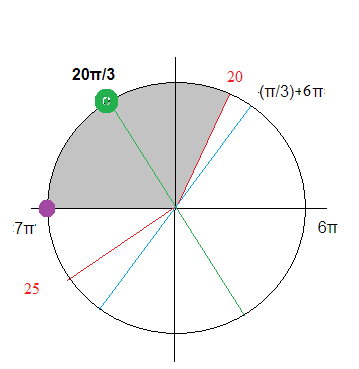
Все решения

