Задача 44452 В треугольнике АВС сторона ВС больше...

slava191

2020-02-22 22:02:13

В треугольнике АВС сторона ВС больше стороны АС. Биссектриса CL пересекает описанную около треугольника АВС окружность в точке К. Окружность, описанная около треугольника AKL вторично пересекает прямую АС в точке Р.

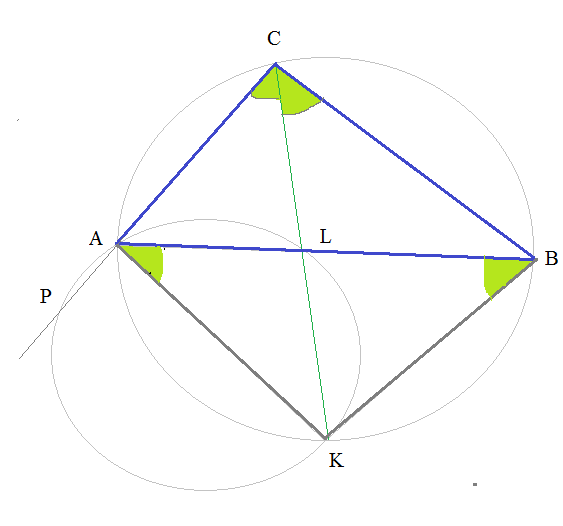
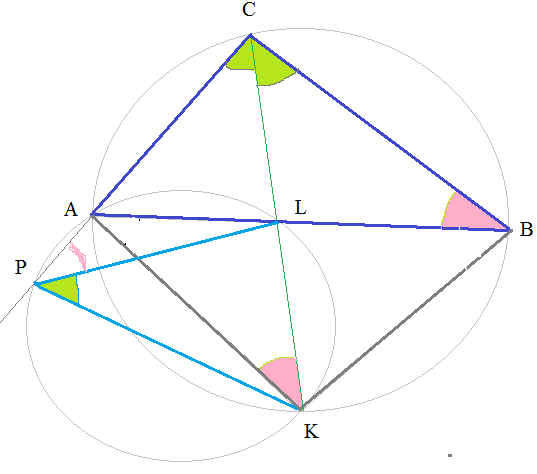
а) Докажите, что отрезки ВС и РС равны.

Б) Найдите площадь треугольника АРК, если ВС=6, АВ=5, АС=4.

sova

2020-02-23 21:20:05

Биссектриса CL делит угол С пополам:
∠ АСL= ∠ DCL

Это вписанные углы, значит и дуги, на которые они опираются тоже равны:
∪ AK= ∪ BK

∠ АВК= ∠ ВАК как углы, опирающиеся на равные дуги.

Δ АВК - равнобедренный ⇒ АК=ВК

∠ АСL= ∠ DCL=∠ АВК= ∠ ВАК

Рассмотрим окружность, описанную около Δ AKL

∠ AKL=∠ АPL⇒ как углы, опирающиеся на ∪ AL

Δ BCL= Δ PCL по общей стороне СL и двум прилежащим к ней углам:

∠ АСL= ∠ DCL
и
∠ AKL=∠ АPL

Из равенства треугольников следует равенство сторон:
ВС=РС


б)
Дано:
ВС=6, АВ=5, АС=4.

ВС=РС=6

АР=РС-АС=6-4=2

Δ АРК :





S_( Δ АКР)=

О т в е т.