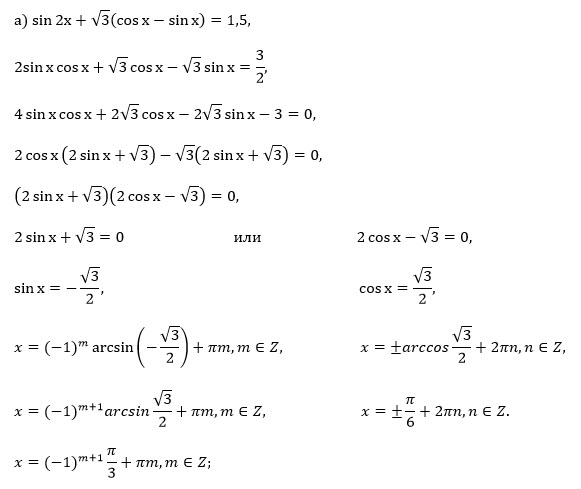Задача 44449 sin2x+sqrt(3)(cosx-sinx) = 1,5; [-7Pi/2;...
Условие
Все решения
2*sinx*cosx+sqrt(3)*cosx-sqrt(3)*sinx=1,5
Умножаем на 2:
4*sinx*cosx+2*sqrt(3)*cosx-2*sqrt(3)*sinx=3;
4*sinx*cosx+2*sqrt(3)*cosx-2*sqrt(3)*sinx-3=0;
Группируем:
(4*sinx*cosx+2*sqrt(3)*cosx)-(2*sqrt(3)*sinx+3)=0;
2*cosx*(2*sinx+sqrt(3))-sqrt(3)(2*sinx+sqrt(3))=0;
(2*sinx+sqrt(3))*(2*cosx-sqrt(3))=0
Произведение равно 0, когда хотя бы один из множителей равен 0,
а другие при этом не теряют смысла.
(в данном уравнении оба множителя имеют смысл при любом х)
2*sinx+sqrt(3)=0 ⇒ sinx=-sqrt(3)/2
x=(-1)^(k)*(-π/3)+πk, k ∈ Z
x=(-π/3)+2πk, k ∈ Z или x=(-2π/3)+2πm, m ∈ Z
2*cosx-sqrt(3)=0 ⇒ cosx=sqrt(3)/2
x= ± (π/6) +2πn, n ∈ Z
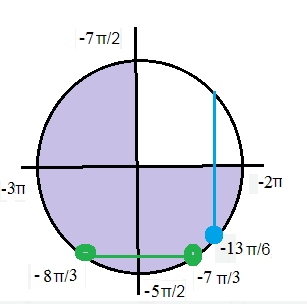
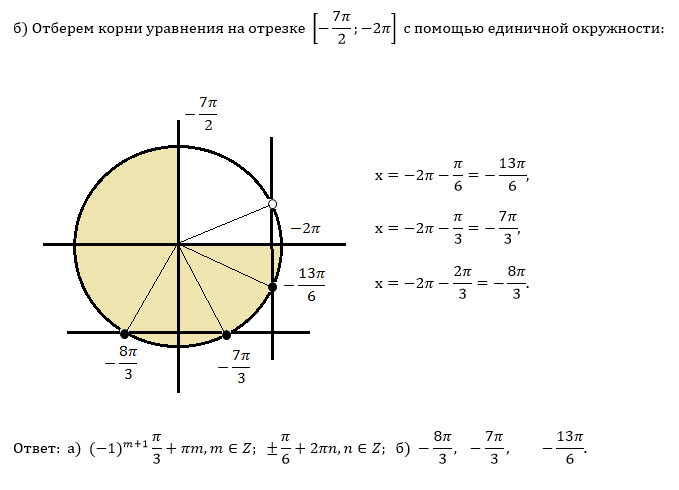
б)
Запишем корни (-1)^(k)*(-π/3)+πk, k ∈ Z
в виде:
(-π/3)+2πm или x=(-2π/3)+2πm, m ∈ Z
Указанному отрезку принадлежат корни при m=-1
[b]-8π/3; -7π/3[/b]
x= ± (π/6) +2πn, n ∈ Z
Указанному отрезку принадлежит корень
- (π/6) -2π=-13π/6
О т в е т.
a)(-1)^(k)*(-π/3)+πk, ± (π/6) +2πn, k,n ∈ Z
б)
[b]-8π/3; -7π/3; -13π/6[/b]