Задача 44394 Решите уравнение ...

saklethil

2020-02-19 23:13:26

Решите уравнение

sova

2020-02-19 23:44:58

★

Правая часть:

25-y^2 ≥ 0 ⇒ -5 ≤ y ≤ 5

0 ≤ sqrt(25-y^2) ≤ 5
0 ≤ 3*sqrt(25-y^2) ≤ 15

5 ≤ 3*sqrt(25-y^2) +5≤ 20

Левая часть

x ≤ -4
9*(-x+1)+4*(-x-4)=-13x-7

-4<x ≤ 1
9*(-x+1)+4*(x+4)=-5x+25

x>1
9*(x-1)+4*(x+4)=13x+7

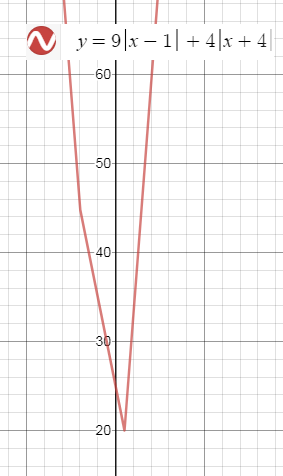
9*|x-1|+4*|x+4| ≥ 20

Поэтому левая часть если и равна правой, то только в случае:
9*|x-1|+4*|x+4|=20 ⇒
x=1

3*sqrt(25-y^2) +5= 20 ⇒ sqrt(25-y^2)=5 ⇒ 25-y^2=25
y^2=0
y=0

О т в е т. (1;0)