Задача 44354 Найти наибольшее и наименьшее значение...
Условие
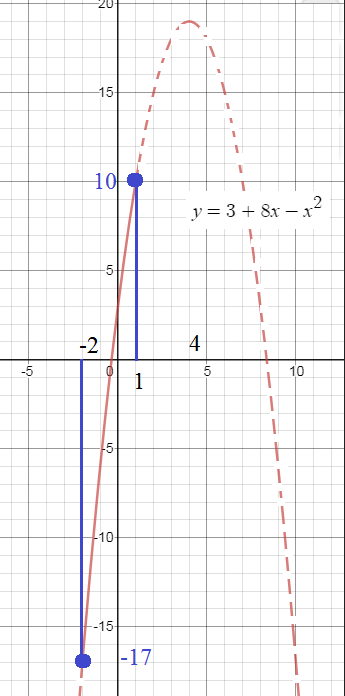
1. y = 3 + 8x - x^2 На отрезке [-2; 1]
2. y = 3x^4 - 4x^3 + 6x^2 - 12x + 8 На отрезке [0; 2]
3. y = 3 + 2x^2 - 8x^3 На отрезке [-2; 0]
Решение



Все решения
y`=8-2x
y`=0
8-2x=0
x=4 - точка возможного экстремума, но она не принадлежит отрезку [-2;1]
Значит функция на этом отрезке [i]монотонна [/i]
( а именно возрастает:y`>0 если 8-2х> 0, т.е при x<4)
[-2;1] ⊂ (- ∞ ;4)
Наибольшее значение в правом конце:
х=1
y(1)=3+8-1=10
Наименьшее значение в левом конце:
х=-2
y(-2)=3+8*(-2)-(-2)^2=-17
см. рисунок.
Нас интересует не весь график функции, а только его часть, расположенная на отрезке [-2;1]
Остальная часть на рис. изображена пунктиром.
Хорошо видно, что х=4 - точка максимума,
находится на участке, который исследованию не подлежит....