Задача 44347 Найдите произведение целых значений...
Условие
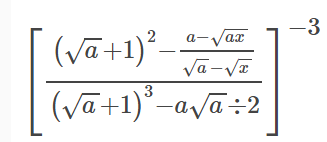
Решение
x ≥ 0
sqrt(a)-sqrt(x) ≠ 0 ⇒ sqrt(x) ≠sqrt(a) ⇒ x≠a
При x=0
[m]\frac{a–\sqrt{0}}{\sqrt{a}–\sqrt{0}}=\frac{a}{\sqrt{a}}[/m] ⇒ a≠0
⇒ x ≠ 0
Получаем, что [red]x >0[/red] и [green] a>0[/green]
Упростим выражение:
[m]\frac{a–\sqrt{ax}}{\sqrt{a}–\sqrt{x}}=\frac{\sqrt{a}\cdot(\sqrt{a}–\sqrt{x}}{\sqrt{a}–\sqrt{x}}=\sqrt{a}[/m]
Выражение не зависит от х:
[m](\frac{a+\sqrt{a}+1}{3a+3})^{-3}=\frac{27(a+1)^3}{(a+\sqrt{a}+1)^3}[/m]
так как
[m](\sqrt{a}+1)^{2}-\sqrt{a}=a+2\sqrt{a}+1-\sqrt{a}=a+\sqrt{a}+1[/m]
[m](\sqrt{a}+1)^{3}–a\sqrt{a}+2=a\sqrt{a}+3a+3 \sqrt{a}+1-a\sqrt{a}+2=3a+3\sqrt{a}+3[/m]
[m](\frac{a+\sqrt{a}+1}{3a+3\sqrt{a}+3})^{-3}=\frac{27(a+\sqrt{a}+1)^3}{(a+\sqrt{a}+1)^3}=27[/m] - получилось число , которое не зависит ни от х, ни от а
Но поскольку x > 0, то ответ на вопрос:
"Найдите произведение целых значений х, принадлежащих промежутку (-5;4)"
такой:
[b]Это x>0 и принадлежащие промежутку (-5;4)[/b]
x=1;2;3;
Произведение 1*2*3
О т в е т. [b]1*2*3=6[/b]