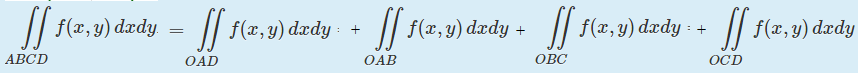Задача 44267 На рисунке изображен квадрат...
Условие
Зная значения интегралов:
[m]
\iint\limits_{OAD} f(x, y)\, dxdy = 2, \\
\iint\limits_{OAB} f(x, y)\, dxdy = 5, \\
\iint\limits_{OBC} f(x, y)\, dxdy = -3, \\
\iint\limits_{OCD} f(x, y)\, dxdy = -1, \\
[/m]
определите значение [m]\iint\limits_{ABCD} f(x, y)\, dxdy[/m].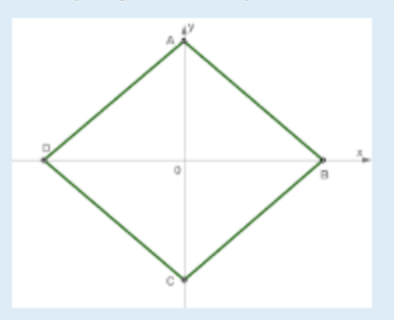
математика ВУЗ
614
Решение
★
Если область интегрирования разбита на несколько "мелких "областей, то
интеграл по области равен сумме интегралов по всем "мелким "
областям
2+5+(-3)+(-1)=[b]3[/b] - о т в е т.