Задача 44123 Вариант 2 1. На рисунке 30, а...
Условие
1. На рисунке 30, а изображена треугольная призма [m] ABC, AB_1C_1, S_1 [/m].
2. Точки [m] O, P [/m] и [m] T [/m] — соответственно середины ребер [m] AS, AB [/m] и [m] BC [/m] треугольной пирамиды [m] SABC [/m]. Прямая [m] l [/m] проходит через точку [m] O [/m] и параллельна прямой [m] AC [/m]. Установите взаимное расположение прямой [m] l [/m] и плоскости [m] SOT [/m].
3. На рисунке 30, г изображена правильная треугольная пирамида [m] SABC [/m]. Точки [m] E [/m] и [m] K [/m] — точки пересечения ребер [m] SB [/m] и [m] SE [/m], [m] BE = 2 : 1 [/m]. Точка [m] K [/m] — середина ребра [m] DC [/m]. Докажите, что [m] EKI \sharp ABC [/m].
4. Длина каждого ребра прямой треугольной призмы [m] ABCA_1B_11C_1 [/m] равна [m] a [/m]. Найдите периметр сечения пирамиды серединными точками сторон треугольника [m] V_0A_0 [/m], [m] B_0 [/m] и прямой [m] BCT_0 [/m].
5. Точки [m] T [/m] — середина [m] E [/m] грани [m] AA_0 [/m], [m] CD [/m], длины граней [m] ABCA_0 [/m], [m] B_0G_0 [/m], E_0 в параллельной [m] S_0 [/m] плоскости его периметра.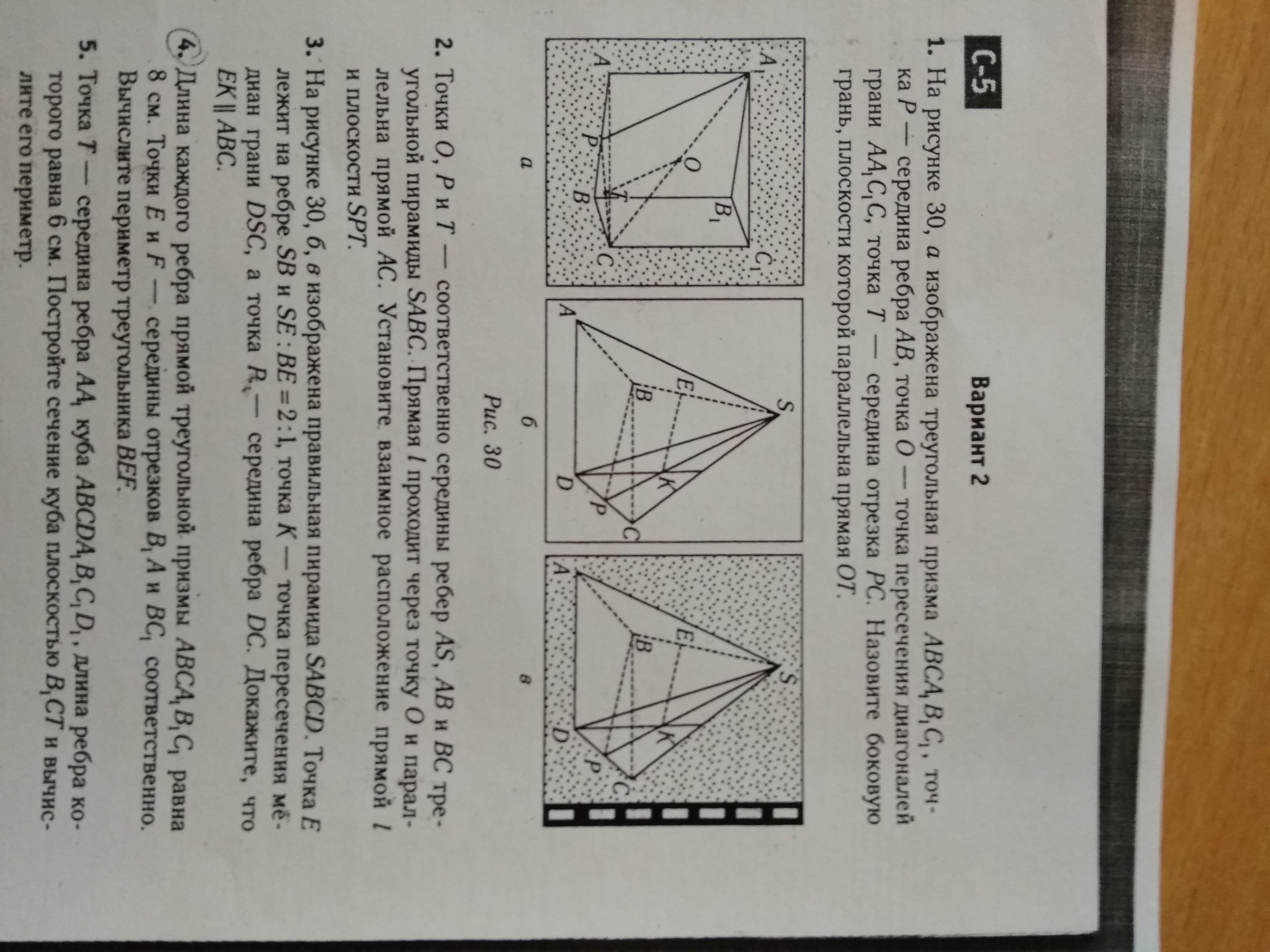
Все решения
АА_(1)В_(1)В
[b]2)[/b] РТ || AC ( РТ - средняя линия Δ АВС)
[i]l[/i] || AC
[i]l[/i] || PT ⇒ l || пл Δ SPT ( cм. признак в приложении)
[b]3)[/b]
SK:KP=2:1 ( медианы в точке пересечения делятся в отношении 2:1)
ЕК || ВР по теореме обратной теореме Фалеса ( или из подобия Δ SBP и ΔSEK)
EK || пл. АВС ( см признак в приложении)
[b]4)[/b] Боковые грани квадраты со стороной 8
АВ_(1)=A_(1)B=8sqrt(2)- диагонали боковой грани АA_(1)В_(1)В
ВС(1)=В_(1)С=8sqrt(2)- диагонали боковой грани BB_(1)С_(1)С
BE=(1/2)A_(1)B=4sqrt(2)
BF=(1/2)BC_(1)=4sqrt(2)
EF - средняя линия Δ АВ_(1)С
EF=AC/2=4
Р( Δ ВЕF)=BE+EF+BF=4sqrt(2)+4+4sqrt(2)=[b]8sqrt(2)+4[/b]
[b]5)[/b]
Соединяем С с В_(1) это линия пересечения секущей плоскости
с гранью ВВ_(1)С_(1)С
Соединяем Т с В_(1) это линия пересечения секущей плоскости
с гранью АА_(1)В_(1)В
Продолжаем АВ до пересечения с ТВ_(1) в точке М
Соединяем М с точкой С
МС - линия пересечения секущей плоскости с пл. основания.
МС пересекает AD в точке Р
P cоединяем с точкой Т
PTB_(1)C - сечение