Задача 44053 37.6. Вычислите предел: 5) [m]\lim_{x...
Условие
5) [m]\lim_{x \to \infty} ( \sin 5x + tg 3x ) [/m];
2) [m]\lim_{x \to 0} \left( \frac{\arcsin x}{3x} + \frac{\sin x}{2x} \right) [/m] ;
4) [m]\lim_{x \to 0} \left( \frac{arctg 3x - \sin 3x}{3x} \right) [/m] ;
6) [m]\lim_{x \to \infty} \left( \frac{2x + 1}{x - 1} + \frac{\sin 6x}{3x} \right) [/m] .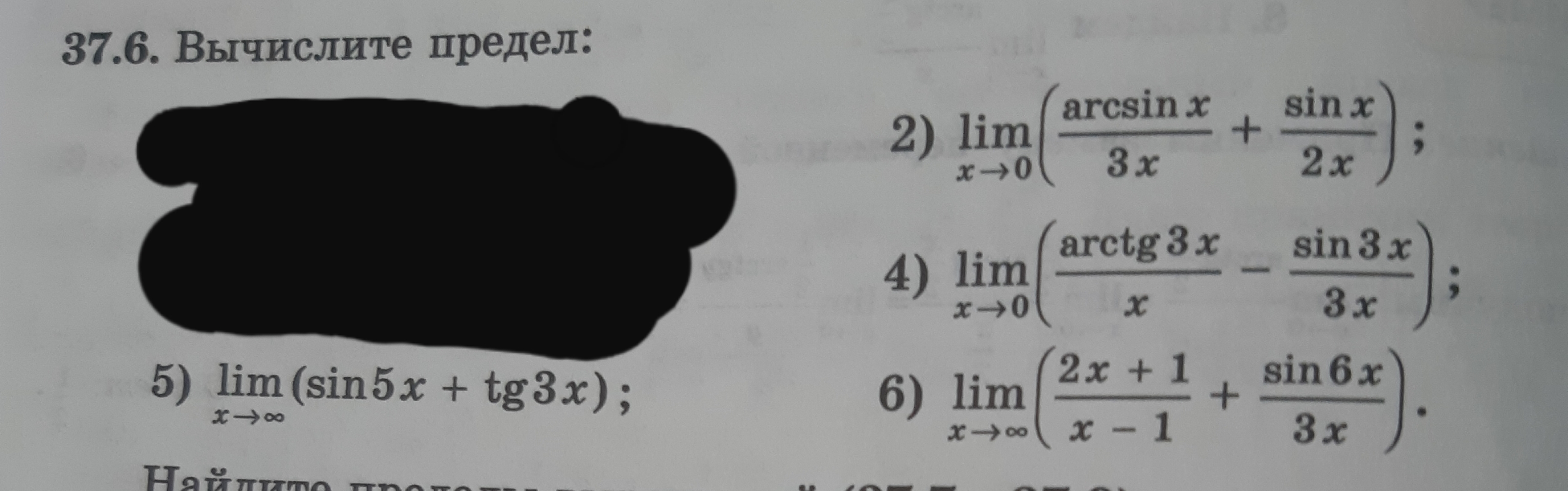
Решение
[m]\lim_{x \to 0 }(\frac{arcsinx}{3x}+\frac{sinx}{2x})=[/m]
предел суммы равен сумме пределов:
[m]=\lim_{x \to 0 }\frac{arcsinx}{3x}+\lim_{x \to 0 }\frac{sinx}{2x}=[/m]
постоянный множитель можно выносить за знак предела:
[m]=\frac{1}{3}\lim_{x \to 0 }\frac{arcsinx}{x}+\frac{1}{2}\lim_{x \to 0 }\frac{sinx}{x}=[/m]
[m]=\frac{1}{3}+\frac{1}{2}=\frac{5}{6}[/m]
[i]Первый замечательный предел:[/i]
[m]\lim_{x \to 0 }\frac{sinx}{x}=1[/m]
[i]Следствие:[/i]
[m]\lim_{x \to 0 }\frac{arcsinx}{x}=1[/m]
3)
[m]\lim_{x \to 0 }(\frac{arctg3x}{x}-\frac{sin3x}{3x})=[/m]
предел разности равен разности пределов:
[m]=\lim_{x \to 0 }\frac{arctg3x}{x}-\lim_{x \to 0 }\frac{sin3x}{3x}=[/m]
Умножим числитель и знаменатель дроби на 3:
[m]=\lim_{x \to 0 }\frac{3arctg3x}{3x}-\lim_{x \to 0 }\frac{sin3x}{3x}=[/m]
постоянный множитель 3 вынесем за знак предела:
[m]=3\lim_{x \to 0 }\frac{arctg3x}{3x}-\lim_{x \to 0 }\frac{sin3x}{3x}=[/m]
[m]=3 - 1 = 2[/m]
[i]Первый замечательный предел:[/i]
[m]\lim_{x \to 0 }\frac{sin3x}{3x}=1[/m]
[i]Следствие:[/i]
[m]\lim_{x \to 0 }\frac{arctg3x}{3x}=1[/m]
5)
Предел каждого слагаемого не существует.
Нет предела.
6)
[m]\lim_{x \to \infty }(\frac{2x+1}{x-1}+\frac{sin6x}{3x})=\lim_{x \to \infty }\frac{2x+1}{x-1}+\lim_{x \to \infty }\frac{sin6x}{3x}=2+0=2[/m]
[m]\lim_{x \to \infty }\frac{2x+1}{x-1}=\frac {\infty } {\infty }=[/m]
делим числитель и знаменатель на х, причем почленно.
Каждое слагаемое числителя делим на х и каждое знаменателя..
[m]\lim_{x \to \infty }\frac{1}{3x}=0[/m]
|sinx| ≤ 1 при любом х ∈ (- ∞ ;+ ∞ )
Произведение бесконечно малой и ограниченной есть бесконечно малая, т. е 0
