Задача 43795 Вычислить пределы функций, не пользуясь...
Условие
дифференциального исчисления.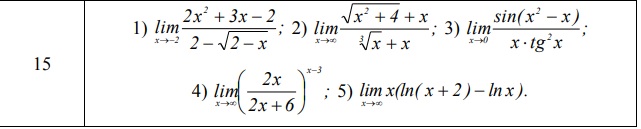
Решение
Неопределенность 0/0
Числитель раскладываем на множители:
2x^2+3x-2=(2x-1)(x+2)
Умножаем и числитель и знаменатель на выражение
2+sqrt(2-x)
Получаем:
[m]=\lim_{x \to -2}\frac{(2x-1)(x+2)(2+\sqrt{2-x})}{(2-\sqrt{2-x})(2+\sqrt{2-x})}=[/m]
Применяем формулу разности квадратов a^2-b^2=(a-b)*(a+b)
[m]\lim_{x \to -2}\frac{(2x-1)(x+2)(2+\sqrt{2-x})}{2^2-(\sqrt{2-x})^2}=\lim_{x \to -2}\frac {(2x-1)(x+2)(2+\sqrt{2-x})}{4- (2-x)}=[/m]
[m]=\lim_{x \to -2}\frac {(2x-1)(x+2)(2+\sqrt{2-x})}{x+2}=[/m]
Сокращаем на ( x+2)
[m]=\lim_{x \to -21}(2x-1)(2+\sqrt{2-x})=(2\cdot (-2) -1)(2+\sqrt{2-(-2)})=[/m]
[m]=-5\cdot 2=-10[/m]
2) Неопределенность ( ∞ / ∞ )
Делим и числитель и знаменатель на x
[m]=\lim_{ \to \infty }\frac{\frac{\sqrt{x^2+4}+x}{x}}{\frac{\sqrt[3]{x}+x}{x}}=[/m]
Делим почленно, те каждое слагаемое числителя делим на x и
каждое слагаемое знаменателя делим на x:
[m]\lim_{ \to \infty }\frac{\frac{\sqrt{x^2+4}}{x}+\frac{x}{x}}{\frac{\sqrt[3]{x}}{x}+\frac{x}{x}}[/m]
Применяем свойства корня:
[m]\lim_{\to \infty }\frac{\sqrt{\frac{x^2+4}{x^2}}+1}{\sqrt[3]{\frac{x}{x^3}}+1}=[/m]
[m]\lim_{\to \infty }\frac{\sqrt{1+\frac{4}{x^2}}+1}{\sqrt[3]{\frac{1}{x^2}}+1}=\frac{\sqrt{1+0}+1}{\sqrt{0}+1}=2[/m]
3) Неопределенность (0/0)
Умножаем и числитель и знаменатель на
(x^2-x)*x^2
[m]\lim_{x\to 0 }\frac{sin(x^2-x)\cdot x^2\cdot (x^2-x))}{x\cdot x^2\cdot (x^2-x)\cdot tg^2x}=[/m]
Применяем cвойства первого замечательного предела:
[m]\lim_{x\to 0 }\frac{sin(x^2-x)}{x^2-x}=1[/m]
[m]\lim_{x\to 0 }\frac{x}{tgx}=1[/m]
[m]\lim_{x\to 0 }\frac{x\cdot x}{tgx\cdot tgx}=1[/m]
[m]\lim_{x\to 0 }\frac{sin(x^2-x)}{(x^2-x)}\cdot \frac{x^2}{tg^2x}\cdot\frac{x^2-x}{x^3} =\lim_{x\to 0 }\frac{x\cdot(x-1)}{x^3}=\lim_{x\to 0 }\frac{x-1}{x^2}=-\infty[/m]
