Задача 43787 ...

79297135371

2020-01-28 23:10:44

Даны уравнения линии r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам на промежутке от (φ)=0 до (φ)=2(π) с шагом, равным (π)/8; 2)найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс- с полярной осью; 3)назвать линию, найти координаты центра и полуоси.

r=4/(2-3cos φ)

sova

2020-01-28 23:31:01

★

В полярной системе координат, откладывают лучи от начала О.
Эти лучи заполняют всю плоскость.

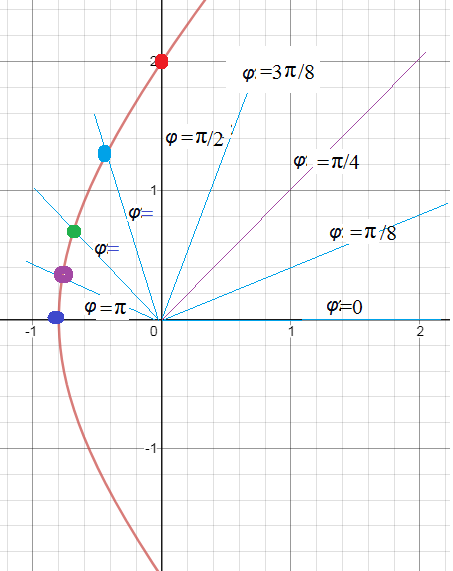
В условии задачи предлагают провести лучи
φ =0
φ =π/8
φ =2π/8=π/4
и так далее.

На каждом таком луче откладывается расстояние.

Например при φ =π/2
откладываем r=4/(2-3*0)=2

На луче откладываем расстояние только в одну сторону, т.е

r ≥ 0

4/(2-3cos φ ) >0 ⇒ 2-3cos φ >0 ⇒[b] cos φ <2/3[/b]


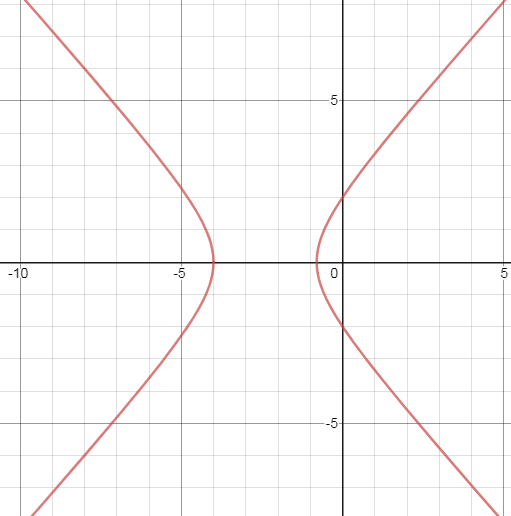
Вообще-то это гипербола.

Надо перейти от полярных координат к декартовым

r=sqrt(x^2+y^2)
cos φ =x/r

⇒
sqrt(x^2+y^2)=4/(2-3*x/sqrt(x^2+y^2))

упростить и получить уравнение в декартовых координатах