Задача 43786 Дано уравнение 4^x+2x= 0. Требуется: 1)...

79297135371

28 января 2020 г. в 22:32

Дано уравнение 4^x+2x= 0. Требуется: 1) графическим методом отделить корень этого уравнения; 2) найти этот корень с точностью до 0,1 методом деления отрезка пополам.

sova

28 января 2020 г. в 22:39

★

4^x=–2x


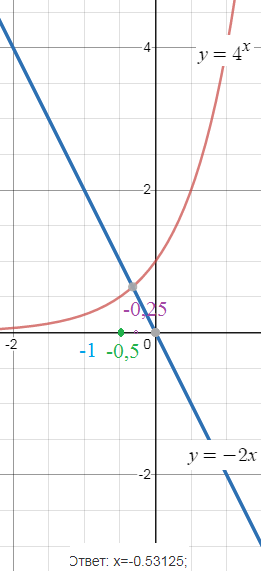
Строим график функции y=4^x и y=–2x

Из рисунка видно, что корень находится на [–0,5;0]


–––––––––––––––––––––––––––––––––


Пусть f(x)=4^x+2x

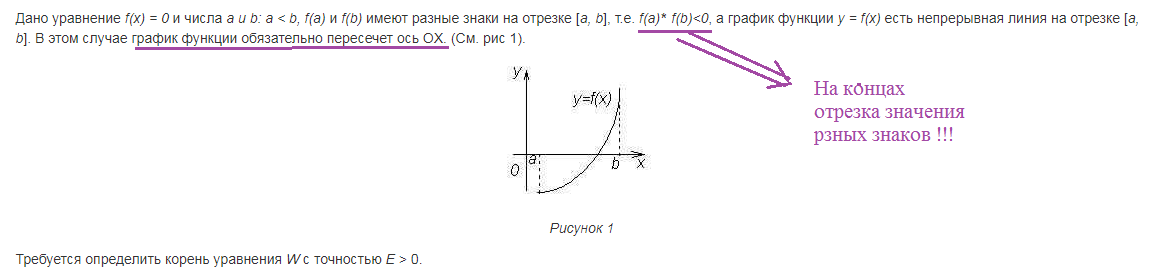
(cм. приложение 2) Постановка задачи.

Если на концах отрезка [–0,5;0] функция y=f(x) имеет разные знаки, то внутри [–0,5;0] находится корень уравнения.


f(–0,5)=4^–0,5+2·(–0,5)<0
f(0)=4⁰+0=1>0

Корень находится на [–0,5;0]


Делим отрезок [–0,5;0]пополам

Получаем два отрезка:

[–0,5;–0,25] и [–0,25;0]

Проверяем корень на принадлежность первому отрезку или второму.

4^–0,25+2·(–0,25)>0

так как
[m]4^{-0,25}=\frac{1}{4^{0,25}}=\frac{1}{\sqrt[4]{4}}=\frac{1}{\sqrt[2]{2}}[/m] ≈ 0,7считаем

–2·(–0,25)=0,5


0,7–0,5>0

Значит, корень на [–0,5;–0,25]

Далее снова делим отрезок пополам.

Получаем два отрезка:

[–0,5;–0,375] и [–0,375;–0,25]

...