Задача 43647 ...

crucianni

2020-01-24 10:02:56

Вычислить двойной интеграл по области D
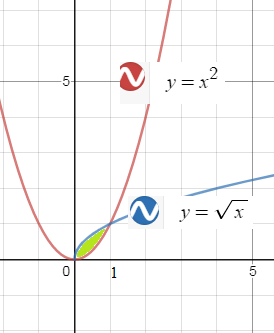
∫ ∫ x^2 ydxdy, D:y=x^2, x=y^2
D

sova

2020-01-24 15:18:58

★

D: 0 ≤ x ≤ 1; sqrt(x) ≤ y ≤ x^2

∫ ∫ x2 ydxdy= ∫^(1)_(0) (∫^(x^2)_(sqrt(x)) x^2dy)dx=
D

= ∫^(1)_(0)x^2*y)|(y=x^2)_(y=sqrt(x))dx=


= ∫^(1)_(0)x^2*(x^2-sqrt(x))dx=

= ∫^(1)_(0)(x^4 - x^(2,5))dx=(x^5/5)|^(1)_(0)- x^(3,5)/(3,5)|^(1)_(0)=

=(1/5)-(1/3,5)=(1/5)-(2/7)=[b]-3/35[/b]