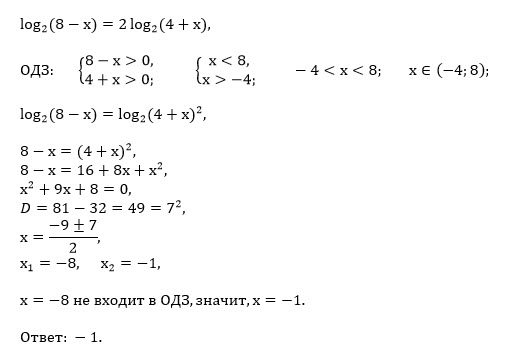Задача 43546 Найдите корень уравнения ...
Условие
Все решения
klog_(c)a=log_(c)a^(k)
( cм. фото в приложении)
[i]Уравнение[/i] принимает вид:
[b]log_(2)(8-x)=log_(2)(4+x)^2[/b]
Логарифмическая функция [b]строго монотонна[/b],
это значит, что каждое свое [i]значение[/i] функция
принимает только [i]один раз.[/i]
Поэтому если значения функции равны, то и аргументы равны:
8-x=(4+x)^2
Раскрываем скобки, приводим подобные слагаемые, получаем квадратное уравнение
x^2+9x +8=0
По теореме[i] Виета[/i] находим корни
x_(1)=-1; x_(2)=-8
Обязательно делаем [red]проверку[/red] ( или находим [green]ОДЗ[/green] вначале решения).
Иногда проверку сделать проще, чем решить систему неравенств в ОДЗ.
При x=-1
log_(2) (8-(-1))=2log_(2)(-1+4)
log_(2)9=2log_(2)3- верно,
т.к log_(2)9=log_(2)3^2=2log_(2)3
При x=-8
log_(2)(-8+4) не существует
О т в е т. x=-1
