Задача 434 В плоскости лежит треугольник ABC, a...
Условие
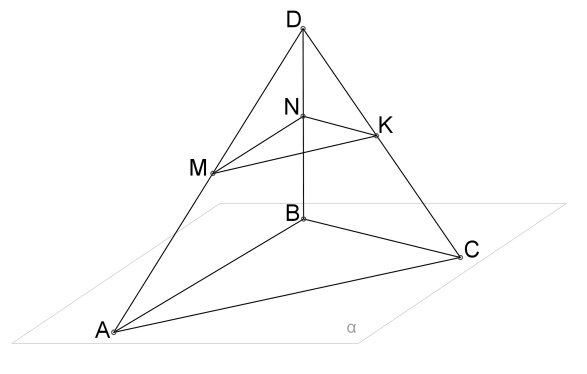
математика 10-11 класс
20769
Решение
Ответ: AB и MN параллельны

Ответ: AB и MN параллельны