Задача 43216 Сторона основания правильной треугольной...

space

2020-01-01 15:37:19

Сторона основания правильной треугольной призмы [m] ABC A_1 B_1 C_1 [/m] равна [m] 8\sqrt{3} [/m] см. На ребре [m] BB_1 [/m] обозначили точку [m] K [/m] так, что [m] BK : KB_1 = 3:5 [/m]. Найти тангенс угла между плоскостями [m] ABC [/m] и [m] AKC [/m], если расстояние между прямыми [m] BC [/m] и [m] A_1 C_1 [/m] равно 16 см. (Искать приближительные значения корней при решении задачи НЕ нужно)

sova

2020-01-02 11:34:11

Расстояние между скрещивающимися прямыми ВС и А_(1)С_(1) это длина общего перпендикуляра, т.е длина СС_(1)

СС_(1)=16

BB_(1)=CC_(1)=16

ВK:KB_(1)=3:5 ⇒ BK=(3/8)BB_(1)=(3/8)*16=6

Проводим
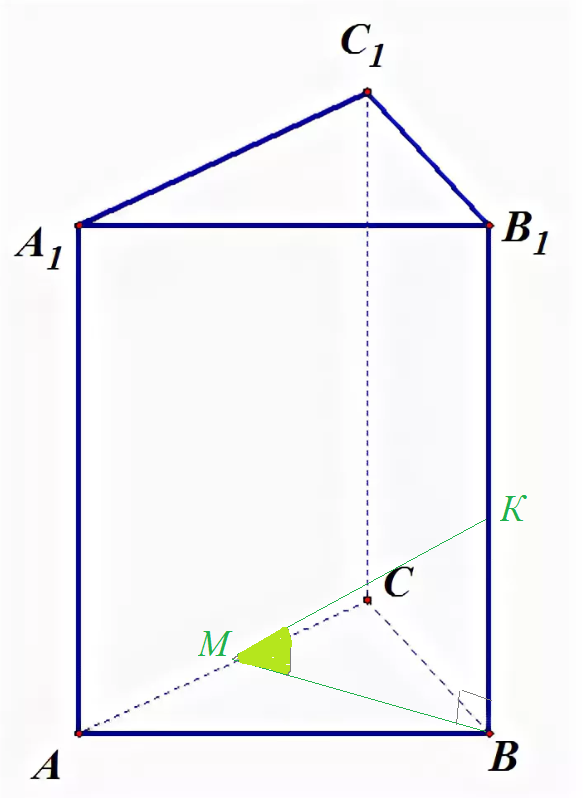
ВМ ⊥ АС
ΔАВС - равносторонний, значит высота ВМ - медиана и биссектриса.
ВМ - проекция КМ на АВС

KM ⊥ AC по теореме о трех перпендикулярах

∠ КМВ - линейный угол двугранного угла между пл АВС и пл АКС)

Из треугольника АВС:

ВМ=АВ*sin ∠CAB=8sqrt(3)*sin60^(o)=8sqrt(3)*(sqrt(3)/2)=12

tg∠ КМВ= BK/BM=6/12=1/2=0,5

О т в е т. 0,5