Задача 43204 Исследовать функцию и построить график...

vk72207933

2019-12-29 18:28:38

Исследовать функцию и построить график y=1/(x^4-1)

sova

2019-12-29 19:57:15

Область определения
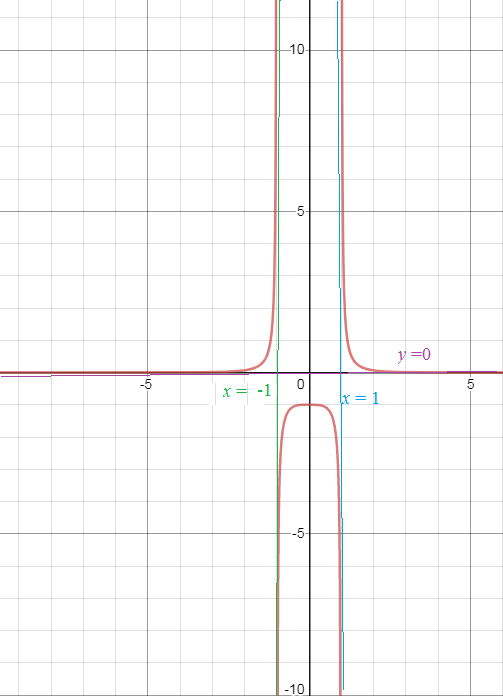
x^4-1 ≠ 0 ⇒ (x^2-1)(x^2+1) ≠ 0 ⇒ x ≠ ± 1

Прямые x= ± 1 - вертикальные асимптоты, так как

lim_(x → 1-0)f(x)= - ∞ и lim_(x → 1+0)f(x)= +∞

и
lim_(x → -1-0)f(x)= +∞ и lim_(x → -1+0)f(x)= -∞

Прямая y=0 - горизонтальная асимптота, так как
lim_(x → ∞ )f(x) = 0

Функция четная, [m]y(-x)=\frac{1}{(-x)^4-1}=\frac{1}{x^4-1}=y(x)[/m]

График симметричен относительно оси Оу

y`=-(1/(x^4-1)^2)*(x^4-1)`= (- 4x^3)/(x^4-1)^2

y`>0 при x ∈ (- ∞ ;-1)и при х ∈ (-1;0)

функция возрастает на (- ∞ ;-1) и на (-1;0)

y`<0 при x ∈ (0 ;1) и при х ∈ (1;+ ∞ )

Функция убывает на (0 ;1) и на (1;+ ∞ )