Задача 432 Построить плоскость параллельную...

slava191

12.01.2014

Построить плоскость параллельную плоскости АВС и расположенную выше её на расстоянии 30 мм.

Построить плоскость параллельную плоскости АВС и расположенную выше её на расстоянии 30 мм.

Для решения задачи введем новую плоскость проекций П4 - горизонтально проецирующую и перпендикулярную плоскости треугольника.

Плоскость АВС проецируется на П4 в прямую линию, проведем из В4 перпендикуляр длинной 30 мм, получим точку К4 и через нее проведем проекцию плоскость (m4n4) параллельную плоскости АВС.

Плоскость параллельна другой плоскости если две прямые одной плоскости соответственно параллельны двум прямым другой плоскости ( пусть m//АВ, а n//BC).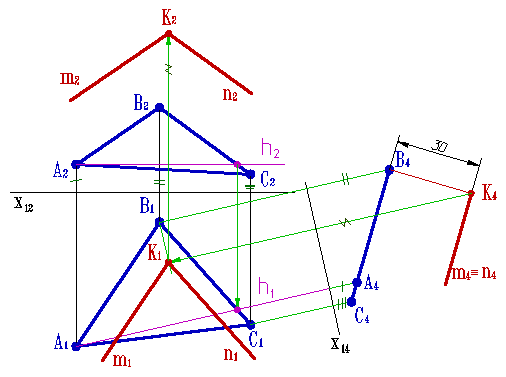

Ответ: построение