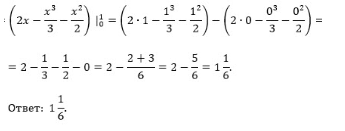Задача 43167 Вычислить площадь фигуры ограниченной...

dimon708

2019-12-27 10:38:24

Вычислить площадь фигуры ограниченной линиями

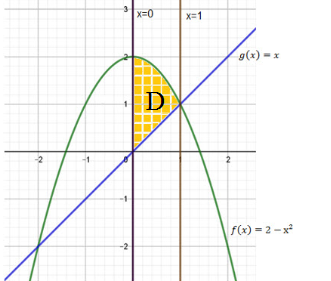
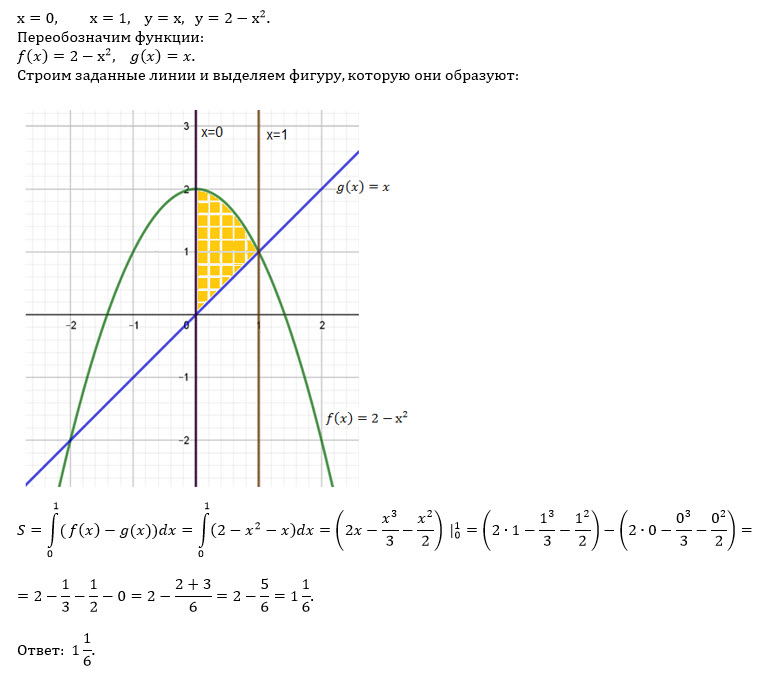
x=0, x=1, y=x, y=2-x^2

sova

2019-12-27 14:53:17

2.Тема Двойной интеграл. Поэтому решение будет выглядеть так:

S= ∫ ∫ _(D)dxdy

D: 0 < x < 1; x < y < 2-x^2

S= ∫ ^(1)_(0)( ∫ ^(2-x^2)_(x)dy)dx= ∫ ^(1)_(0)(y|^(2-x^2)_(x))dx=

= ∫ ^(1)_(0)(2-x^2-x)dx=