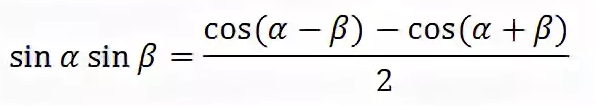Задача 42925 Найти точки экстремума f(x) =...

vk226434676

2019-12-20 08:40:49

Найти точки экстремума f(x) = x^3-3x^2-sin(Pi/4)

sova

2019-12-20 13:15:00

★

3.1
f`(x)=(x^3-3x^2-sin(π/4))`=(x^3)`-3*(x^2)`-(sin(π/4))`=3x^2-3*2x-0=3x^2-6x

f`(x)=0

3x^2-6x=0

3x*(x-2)=0

x=0 или x=2

Знак производной:

_+__ (0) __-__ (2) __+__


х=0 - точка максимума, производная меняет знак с + на -

х=2- точка минимума, производная меняет знак с - на +

2.
Так как

sin7x*sin5x=(cos(2x)-cos(12x))/2=(1/2)cos2x-(1/2)cos12x, то



∫ sin7x*sin5x dx=(1/2) ∫ cos2xdx-(1/2) ∫ cos12xdx=

[b]=(1/4)sin2x-(1/24)sin12x+C[/b]