Задача 42759 ...
Условие
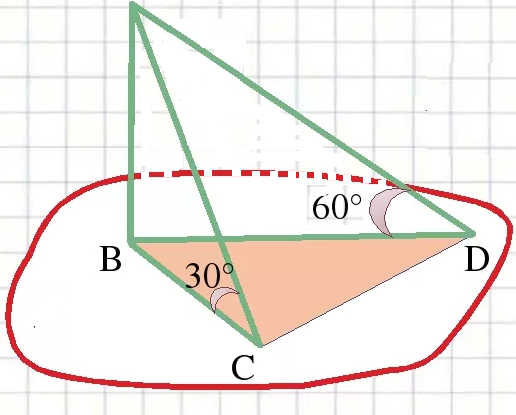
1. Дан АВ - перпендикуляр к плоскости a,AC и AD - наклонные, проведенные по разные стороны от перпендикуляра . кв.ACB =30°,кв.ADB=60°,AC=24Найдите проекции наклонных на плоскость a и длину второй наклоннойAD .
2. В прямоугольном параллелепипеде ширина, длина и высота равны соответственно 12см,16см, 20√3см. Найдите угол между диагональю параллелепипеда и плоскостью основания.
3. Ребро CD тетраэдра ABCD перпендикулярно к плоскости ABC , AB=BC=AC=12,BD=6√7. Найдите угол между плоскостями ABD и ABC. Определите расстояние от точки D до прямой AB.
4. Плоскости равнобедренных треугольников ABD и ABC с общим основанием перпендикулярны.AD=10 cm ,AB=16cm , кв.ACB=60° . Найдите CD .
Решение
Из прямоугольного треугольника АСВ ( АВ ⊥ пл. ⇒ АВ ⊥ ВС, ∠AВC=90 градусов)
АВ=АС/2=12 cм ( катет против угла в 30 градусов равен половине гипотенузы)
ВС^2=AC^2-AB^2=24^2-12^2=432
BC=12sqrt(3)
Из прямоугольного треугольника АDВ ( АВ ⊥ пл. ⇒ АВ ⊥ ВD, ∠ AВD=90 градусов)
∠ BAD=90 градусов-60 градусов=30 градусов
BD=x
AD=2x
Катет BD против угла в 30 градусов равен половине гипотенузы AD
AD^2=AB^2+BD^2
(2x)^2=12^2+x^2
3x^2=144
x^2=48
x=4sqrt(3)
BD=4sqrt(3)
AD=8sqrt(3)