Задача 42642 ...
Условие
2) lim (x→π/3) (sin x + cos 2x) / √(1 + x²)
3) lim (x→1) (x³ - 3x² + 2) / (x² - 4x + 3)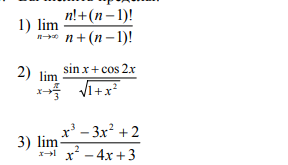
математика ВУЗ
635
Решение
★
=(1+0)/(0+0)=1/0= ∞
2) = (sin(π/3)+2cos(π/3))/(sqrt(1+(π/3)^2)=(sqrt(3)/2 + 2*(1/2))/(1+(π^2/9))=9*(sqrt(3)+2)/(2*(9+π^2))
3)Неопределенность (0 /0 )
Значит х=1 - корень и числителя и знаменателя. Надо сократить и числитель и знаменатель на (х-1)
Для этого надо разложить и и числитель и знаменатель
на множители:
x^3-3x+2=(x-1)*(x^2+x-2)
x^2-4x+3=(x-1)(x-3)
=lim_(x → 1)(x^2+x-2)/(x-3)=(1+1-2)/(1-3)=0/(-2)=0
