Задача 42638 ...
Условие
f(x) = { x, 0 ≤ x < π/2,
{ 0, π/2 ≤ x < π.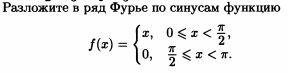
Решение
Находим b_(k) ( cм. приложение)
[m]b_{k}=\frac{2}{\pi }\int^{\pi }_{0} f(x)sinkxdx=\frac{2}{\pi }\int ^{\frac{\pi }{2}}_{0}x\cdot sinkxdx+\frac{2}{\pi }\int^{\pi} _{\frac{\pi }{2}}0\cdot sinkxdx[/m][red]=[/red]
Интегрирование по частям
u=x
dv=sinkxdx ⇒
du=dx
v= ∫ sinkxdx =[m]\frac{1}{k}[/m](-coskx)
[red]=[/red] [m]\frac{2}{\pi }\cdot(-\frac{x}{k}coskx)|^{\frac{\pi }{2}}_{0}+\frac{2}{\pi }\cdot \frac{1}{k}\int ^{\frac{\pi }{2}}_{0}coskxdx=[/m]
[m]\frac{2}{\pi }\cdot(-\frac{\frac{\pi }{2}}{k}cos\frac{\pi }{2}k-0)+\frac{2}{\pi k^2}(sinkx)|^{\frac{\pi }{2}}_{0}=[/m]
[m]=-\frac{1}{k}\cdot cos\frac{\pi }{2}k+\frac{2}{\pi k^2}sin\frac{\pi }{2}k
[/m][green]=[/green]
[blue]при k=2n-1[/blue]
[m]cos\frac{\pi }{2}k=0[/m]
[m]sin\frac{\pi }{2}k=sin\frac{\pi }{2}(2n-1)=sin(\pi n-\frac{\pi }{2})=-cos\pi n=-(-1)^{n}=[/m]
[m]=(-1)^{n+1}[/m]
[blue]при k=2n[/blue]
[m]cos\frac{\pi }{2}2n=cos\pi n=(-1)^{n}[/m]
[m]sin\frac{\pi }{2}k=sin\frac{\pi }{2}\cdot 2n=sin\pi n=0[/m]
