Задача 42608 Найдите область сходимости ряда...
Условие
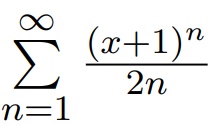
Решение
находим
[m]\lim_{n \to \infty }\frac{|u_{n+1}(x)|}{|u_{n}(x)|}=\lim_{n \to \infty }\frac{\frac{|x+1|^{n+1}}{2(n+1)}}{\frac{|x+1|^{n}}{2n}}= |x+1|\lim_{n \to \infty }\frac{2n}{2n+1}=|x+1|[/m]
Если
|x+1| < 1 ряд сходится,
т.е при -2 < x < 0
При x=-2
получаем знакочередующийся числовой ряд ∑ ^( ∞ )_(1)(-1)^n/2n, который сходится по признаку Лейбница
|а_(n)|=1/2n → 0 при n → ∞
и
числовая последовательность
{|a_(n)|}^(+ ∞ )_(1)={1/(2n)} ^(+ ∞ )_(1)монотонно убывает,
потому что функция
f(x)=1/(2x) -монотонно убывает,потому что проивзодная функции
f`(x)=-1/(2x^2) < 0
f(n)=|a_(n)|
При x=0
получаем числовой ряд ∑ ^( ∞ )_(1)1/(2n)=(1/2)*∑ ^( ∞ )_(1)1/n,
который расходится, так как расходится гармонический ряд ∑ ^( ∞ )_(1)1/n,
умножение ряда на константу не влияет на его сходимость