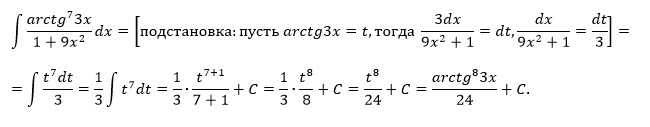Задача 42591 ...
Условие
Подстановка u=arctan(3x) ⟶ du/dx=3/(1+9x^2) ⟶ dx=(1+9x^2)/3du:
=1/3∫u^7du
Теперь вычисляем: u^7du
Интеграл от степенной функции:
∫u^ndu=u^(n+1)/n+1 при n=7:
=u^8/8
Подставим уже вычисленные интегралы:
1/3∫u^7du
=u^8/24
Обратная замена u=arctan(3x):
=〖arctan〗^8 (3x)/24+C
ПРЕПОДАВАТЕЛЮ НЕ НРАВИТСЯ ОБОЗНАЧЕНИЯ ПОМОГИТЕ ПРАВИЛЬНО РЕШИТЬ и ОФОРМИТЬ
математика 8-9 класс
909
Решение
★