Задача 42564 На оси абсцисс найдите такую точку Х...
Условие
M(-3;-2) N(4;-5)
Все решения
Пусть X(x;0)
MX=sqrt((x+3)^2+(0+2)^2)=sqrt(x^2+6x+13)
NX=sqrt((x-4)^2+(0+5)^2)=sqrt(x^2-8x+41)
сумма расстояний:
MX+NX=sqrt(x^2+6x+13)+sqrt(x^2-8x+41) -
функция, зависящая от х
Обозначим
[b]f(x)=sqrt(x^2+6x+13)+sqrt(x^2-8x+41)[/b]
x^2+6x+13 >0 при любом х, так как D=36-4*13 <0
x^2-8x+41>0 при любом х, так как D=64-4*41 <0
Переформулировка задачи:
[i]Найти x, при котором f(x) принимает наименьшее значение.[/i]
По формуле:
(sqrt(u))`=[m]\frac{u`}{2\sqrt{u}}[/m]
f`(x)=[m]\frac{2x+6}{2\cdot \sqrt{x^2+6x+13}} +\frac{2x-8}{2\cdot \sqrt{x^2-8x+41}}[/m]
f`(x)=[m]\frac{x+3}{\sqrt{x^2+6x+13}} +\frac{x-4}{\sqrt{x^2-8x+41}}[/m]
f`(x)=0
[m]\frac{x+3}{\sqrt{x^2+6x+13}} +\frac{x-4}{\sqrt{x^2-8x+41}}[/m]=0
[m]\frac{x+3}{\sqrt{x^2+6x+13}} =-\frac{x-4}{\sqrt{x^2-8x+41}}[/m]
Возводим в квадрат при условии
{x+3 ≥ 0 ⇒ x ≥-3 [red]⇒ [/red]
{-(x-4) ≥ 0 ⇒ x ≤ 4 [red]⇒ [/red]
{[m]\frac{(x+3)^2}{x^2+6x+13}=\frac{x-4)^2}{x^2-8x+41}[/m]
[red]-3 ≤ x ≤ 4[/red]
К третьей строчке применяем основное свойство пропорции:
[b](x+3)^2*(x^2-8x+41)=(x^2+6x+13)*(x-4)^2 [/b]
([green]x^2+6x[/green]+9)*([blue]x^2-8x[/blue]+41)=([green]x^2+6x[/green]+13)*([blue]x^2-8x[/blue]+16)
Сделаем замену переменной:
x^2+6x+9=u
x^2-8x+16=v
u*(v+25)=(u+4)*v
uv+25u=uv+4v ⇒
[blue]25u=4v[/blue]
25*(x^2+6x+9)=4*(x^2-8x+16)
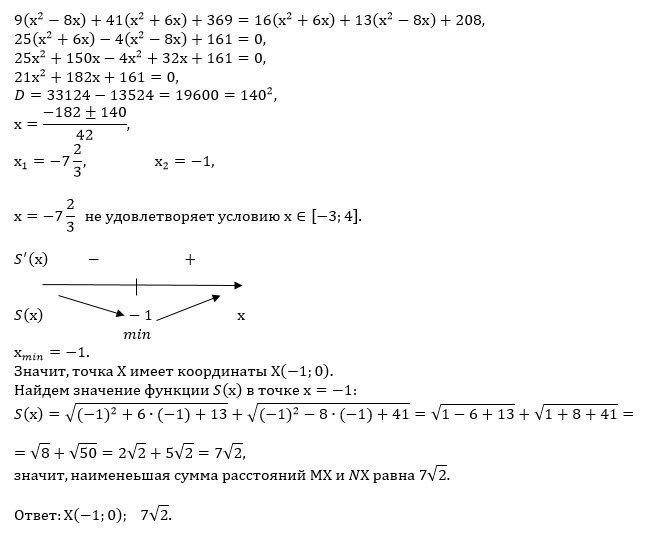
[b]21x^2+182x+161=0[/b]
D=182^2-4*21*161=19600
x_(1)=(-182+140)/42=-1; x_(2)=(-182-140)/42 ∉[ -3; 4]
Применяем достаточное условие экстремума.
[-3] __-__ (-1) ____+___ [4]
x=-1 - точка минимума, производная меняет знак с - на +
f(-1)=sqrt((-1)^2+6*(-1)+13)+sqrt((-1)^2-8*(-1)+41)=
=sqrt(8)+sqrt(50)=2sqrt(2)+5sqrt(2)=7sqrt(2)
это и есть наименьшее расстояние d
О т в е т. [b]Х (-1; 0)[/b]
[b]d=7sqrt(2)[/b]