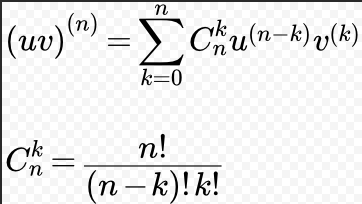Задача 42314 Вычислить y^(18) функции y= x ln...
Условие
Решение
x`=1
ln((3+x)/(3-x))=ln(3+x)-ln(3-x)
(ln((3+x)/(3-x))`=(ln(3+x))`-(ln(3-x))`=1/(3+x) -(-1)/(3-x)
[blue]y`=ln((3+x)/(3-x))+x*((1/(3+x) -(-1)/(3-x))[/blue]
y``=(ln((3+x)/(3-x)))`+((1/(3+x) -(-1)/(3-x))+x*((1/(3+x) -(-1)/(3-x))`
=1/(3+x) -(-1)/(3-x)+((1/(3+x) -(-1)/(3-x))+x*(-(1)/(3+x)^2-(1)/(3-x)^2)
=[green]2/(3+x)+(2/(3-x))+x*(-(1)/(3+x)^2-(1)/(3-x)^2)[/green]
y```= (y``)`
И так 18 раз
Можно найти какую- то закономерность
Вообще для вычисления производной произведения высших порядков применяют формулу Лейбница ( см. рисунок)
n=18
u=x
v=ln((3+x)/(3-x))=ln(3+x)-ln(3-x)
u`=1
u``=0
Все производные до 18-го порядка равны 0
Значит в формуле (u*v)^(18) всего два слагаемых:
(u*v)^(18)=1*u*v^(18)+18*u`*v^(17)
Значит, надо найти[blue] v^(17)[/blue] и[green] v^(18)[/green]
v`=(ln((3+x)/(3-x)))`=(ln(3+x)-ln(3-x))`=(ln(3+x))`-(ln(3-x))`=
=1/(3+x) -(-1)/(3-x)=(1/(3+x))+(1/(3-x))
v``=(1/(3+x))`+(1/(3-x))`=-1/(3+x)^2+1/(3-x)^2
v```=2/(3+x)^3 +2/(3-x)^3
v````=2*(-3)/(3+x)^4 - (2*(-3))/(3-x)^4
....
[blue]v^(17)=16!/(3+x)^(17) +16! /(3-x)^(17)[/blue]
[green]v^(18)=-17!/(3+x)^(18) +17! /(3-x)^(18)
[/green]
О т в е т. y^(18)=x*[b]([/b]-17!/(3+x)^(18) +17! /(3-x)^(18)[b])[/b]+18*[b]([/b]16!/(3+x)^(17) +16! /(3-x)^(17)[b])[/b]