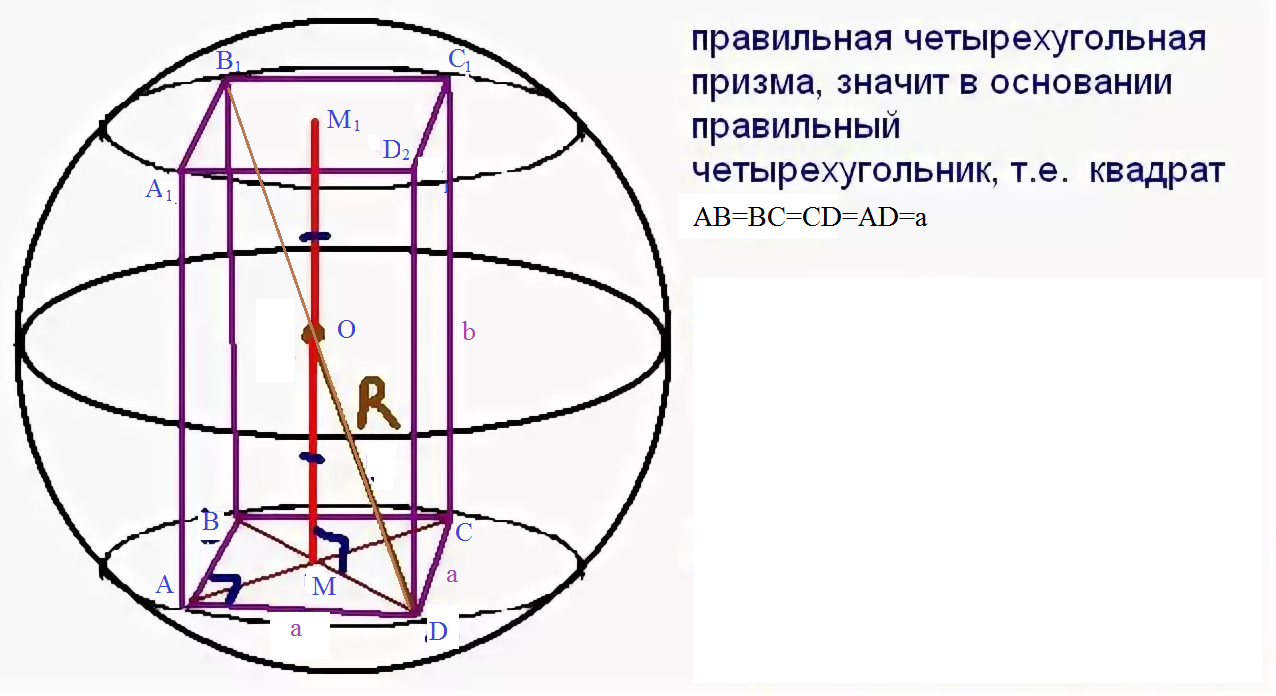
Задача 42313 Найти сторону основания a и боковое...

eximiushero

2019-12-05 21:40:02

Найти сторону основания a и боковое ребро b правильной четырехугольной призмы, вписанной в сферу единичного радиуса и имеющей среди всех таких призм наибольшую полную поверхность

sova

2019-12-05 22:22:29

★

S_(полн)=S_(бок.)+2S_(осн)=4a*b+2*a^2

B_(1)D^2=BB^2_(1)+BD^2=BB^2_(1)+AD^2+AB^2

B_(1)D=2R_(сферы)=2

2=b^2+a^2+a^2 ⇒ b=sqrt(2-2a^2)

Тогда
S_(полн)=4a*b+2*a^2=4a*sqrt(2-2a^2)+2a^2

S_(полн) (а)=4a*sqrt(2-2a^2)+2a^2 - [i]зависит[/i] от а

Исследуем функцию на экстремум.

Пусть a=x
0 < x < 2 ( т. к сторона квадрата не превышает диаметра шара)

S(x)=4x*sqrt(2-2x^2)+2x^2

Находим производную:

S`(x)=4*sqrt(2-2x^2)+4x*(-4x)/2sqrt(2-2x^2)+4x

S`(x)=sqrt(2-2x^2)+x*(-2x)/sqrt(2-2x^2)+x

S`(x)=0

x*sqrt(2-2x^2)=4x^2-2

Возводим в квадрат:

x^2*(2-2x^2)=16x^4-16x^2+4

18x^4-18x^2+4=0

9x^4-9x^2+2=0

D=81-4*9*2=9

x_(1)=(9-3)/18=1/2; x_(2)=(9+3)/18=2/3


S(1/2)=4*(1/2)*sqrt(2-2*(1/2)^2)+2*(1/2)^2=sqrt(6)+(1/2)

S(2/3)=4*(2/3)*sqrt(2-2*(2/3)^2)+2*(2/3)^2=8*(sqrt(10)+1)/9


Cравним:

S(1/2) < S (2/3)

x=a=2/3
b^2=2-2a^2=2-2*(4/9)=10/9
b=sqrt(10)/3


О т в е т. a=2/3; b=sqrt(10)/3