Задача 42311 ...

silikatu9

5 декабря 2019 г. в 20:05

7. Вычислить координаты вершин ромба, если известны уравнения двух его сторон (x + 2y = 4 и x + 2y = 10) и уравнение одной из его диагоналей y = x + 2.

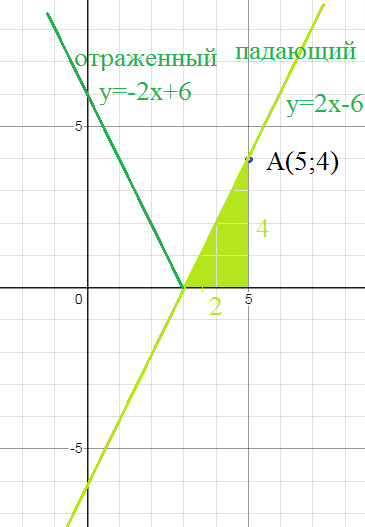
8. Из точки A(5, 4) выходит луч света под углом φ = arctg2 к оси Ох и от нее отражается. Написать уравнения падающего и отраженного лучей.

9. Под каким углом к оси Ох наклонена прямая, проходящая через точки A (1, 4), B (3, 5).

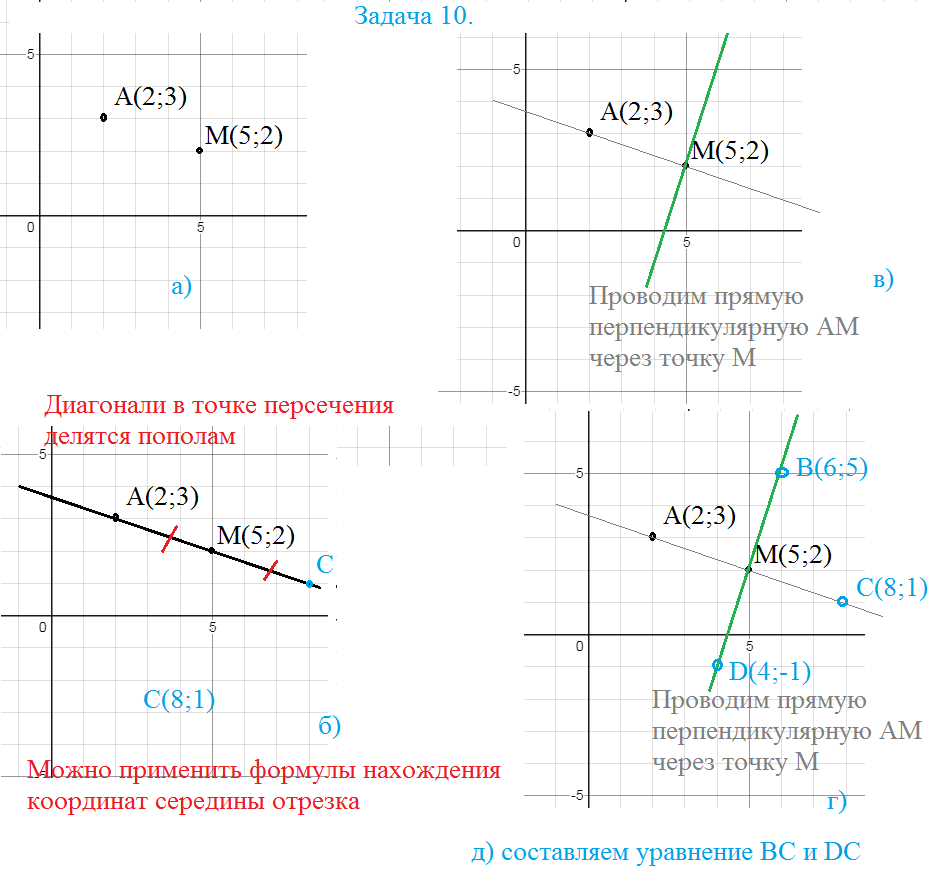
10. В квадрате ABCD даны вершина A (2, 3) и точка М (5, 2) – точка пересечения диагоналей. Найти уравнения сторон квадрата, не проходящих через верши­ну A.

11. Даны точки А (1, 5), В (6, 9), С (7, 2). Отрезок АС разделен точкой D в отношении AD/DC = 2. Найти расстояние от точки A до прямой BD.

sova

5 декабря 2019 г. в 20:11

7. Найти точки пересечения сторон и диагоналей.
Решить две системы уравнений:
{x+2y=4
{y=x+2

{x+2y=10
{y=x+2

Диагонали в точке пересечения делятся пополам.
Найти координаты середины– точки О

Диагонали ромба взаимно перпендикулярны.
Написать уравнение прямой, перпендикулярной y=x+2 и проходящей через точку О.
y=?
Найти точки пересечения этой прямой со сторонами.
Решить две системы уравнений:
{x+2y=4
{y=?

{x+2y=10
{y=?

8.

Уравнение прямой у=kx+b
Геометрический смысл коэффициента k:
k=tg α
α – угол, образованный этой прямой с положительным направлением оси Ох

α =arctg 2 ⇒ tg α =2 ⇒ k=2, b неизвестно

y=2x+b

Так как прямая проходит через точку А(5;4)

Подставляем координаты точки в уравнение:

4=2·5+b
b=–6

О т в е т. y=2x–6 – падающий, отраженный : y=–2x+6

9.
Составляем уравнение прямой, проходящей через две точки
А и В:
[m]\frac{x-x_{B}}{x_{A}-x_{В}}=\frac{y-y_{В}}{y_{A}-y_{В}}[/m]

Подставляем координаты точек

Упрощаем уравнение и приводим к виду
y=kx+b

k=tg α ⇒ находим угол α