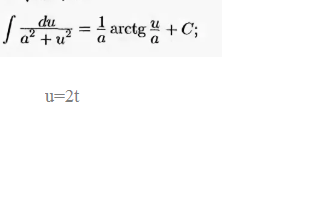Задача 42071 ...

vk131037300

29 ноября 2019 г. в 14:21

Вычислить интеграл табличной подстановкой

∫ dx / (1 + 3 cos² x)

sova

29 ноября 2019 г. в 14:38

★

f(–cosx;sinx)=f(cosx;sinx) – подынтегральная функция четна относительно косинуса, поэтому применяется подстановка

tgx=t ⇒ 1+tg²x=[m]\frac{1}{cos^2x}[/m] ⇒ cos²x=[m]\frac{1}{1+tg^2x}[/m]

cos²x=[m]\frac{1}{1+t^2}[/m]

x=arctgt

dx=[m]\frac{dt}{1+t^2}[/m]

[m]\int \frac{dx}{1+3cos^2x}=\int \frac{\frac{dt}{1+t^2}}{1+3\cdot\frac{1}{1+t^2}}=\int \frac{dt}{1+t^2+3}=\int \frac{dt}{t^2+4}=[/m]

[m]=\frac{1}{2}\cdot arctg\frac{t}{2}=\frac{1}{2}\cdot arctg\frac{tgx}{2}+C[/m]– о т в е т